题目内容
【题目】已知O是锐角△ABC的外接圆的圆心,且∠A= ![]() ,若
,若 ![]()
![]() +
+ ![]()
![]() =2m
=2m ![]() ,则m=( )
,则m=( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:取AB中点D,则有 ![]() =
= ![]() +
+ ![]() ,代入已知式子可得
,代入已知式子可得 ![]()
![]() +
+ ![]()
![]() =2m(
=2m( ![]() +
+ ![]() ),
),
由 ![]() ⊥
⊥ ![]() ,可得
,可得 ![]()
![]() =0,
=0,
∴两边同乘 ![]() ,
,
化简得: ![]()
![]() 2+
2+ ![]()
![]()
![]() =2m(
=2m( ![]() +
+ ![]() )
) ![]() =2m
=2m ![]()
![]() =m
=m ![]() 2 ,
2 ,
即 ![]() c2+
c2+ ![]() bccosA=mc2 ,
bccosA=mc2 ,
由正弦定理化简可得 ![]() sin2C+
sin2C+ ![]() sinBsinCcosA=sin2C,
sinBsinCcosA=sin2C,
由sinC≠0,两边同时除以sinC得:cosB+cosAcosC=msinC,
∴m= ![]() =
= ![]() =sinA=sin
=sinA=sin ![]() =
= ![]()
故选:B.
【考点精析】解答此题的关键在于理解平面向量的基本定理及其意义的相关知识,掌握如果![]() 、
、![]() 是同一平面内的两个不共线向量,那么对于这一平面内的任意向量
是同一平面内的两个不共线向量,那么对于这一平面内的任意向量![]() ,有且只有一对实数
,有且只有一对实数![]() 、
、![]() ,使
,使![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】随着生活水平的提高,越来越多的人参与了潜水这项活动。某潜水中心调查了100名男姓与100名女姓下潜至距离水面5米时是否会耳鸣,下图为其等高条形图:
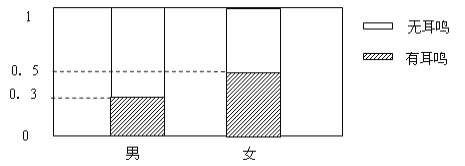
绘出2×2列联表;
②根据列联表的独立性检验,能否在犯错误的概率不超过0.05的前提下认为耳鸣与性别有关系?
| 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
附:![]()
![]()