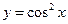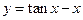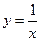题目内容

若f（x）=x3+2x，则曲线y=f（x）在点（1，f（1））处的切线方程为（　　）
A．5x-y-2=0B．5x-y+2=0C．5x+y-2=0D．3x+y-2=0
y'=3x2+2，
y'|x=1=5，切点为（1，3）
∴曲线y=x3+2x在点（1，f（1））切线方程为y-3=5（x-1），
即5x-y-2=0．
故选A．
练习册系列答案
相关题目
设函数f（x）=x3+x2，曲线y=f（x）在点（2，f（2））处的切线方程______．
已知函数f（x）=-x2+ax+1-lnx．
（Ⅰ）若f（x）在x=1处取得极值，求a的值；
（Ⅱ）若f（x）既有极大值又有极小值，求a的取值范围．
设曲线f（x）=ax2+4，若x=1处切线斜率为2，则a的值为（　　）
A．1B．-1C．2D．-2
已知曲线y=x2上一点P处的切线与直线2x-y+1=0平行，则点P的坐标为（　　）
A．（-1，1）B．（1，1）C．（2，4）D．（3，9）
曲线y=x3+1在点（-1，0）处的切线方程为（　　）
A．3x+y+3=0B．3x-y+3=0C．3x-y=0D．3x-y-3=0
若函数y=
x3
3
-x2+1（0＜x＜2）的图象上任意点处切线的倾斜角为α，则α的最小值是（　　）
A．
π
4
B．
π
6
C．
5π
6
D．
3π
4
已知函数f（x）=x3-4x2+5x-4．
（1）求曲线f（x）在x=2处的切线方程；
（2）求经过点A（2，-2）的曲线f（x）的切线方程．
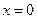下列函数中，是极值点的函数是（       ）
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网