Question

【题目】已知函数f（x）=loga（a＞0且a≠1）是奇函数，

（1）求实数m的值；

（2）若a=，并且对区间[3，4]上的每一个x的值，不等式f（x）＞（）x+t恒成立，求实数t的取值范围．

（3）当x∈（r，a-2）时，函数f（x）的值域是（1，+∞），求实数a与r的值．

Answer 1

【答案】（1）；（2）；（3）.

【解析】

（1）由已知可得恒成立，求出后验证定义域得答案；

（2）时，等价于，令，利用单调性求出在区间，上的最小值可得的范围；

（3）设，则，然后分和两类求解得答案．

解：（1）由f（x）=loga（a＞0且a≠1）是奇函数，

得f（-x）+f（x）=loga+loga==0对于定义域内的任意x恒成立，

即，得m2=1，即m=±1．

当m=-1时，原函数化为f（x）=，定义域为{x|x≠1}（舍去），

∴m=1；

（2）a=时，f（x）＞（）x+t等价于f（x）-（）x＞t，

令g（x）=f（x）-（）x，

则g（x）在区间[3，4]上递增，，

故t＜；

（3）设u=1+，则y=logau，

①当a＞1时，∵函数f（x）的值域是（1，+∞），即y＞1，

∴u=1+（r＜x＜a-2）的值域为（a，+∞），

作出函数u=1+（r＜x＜a-2）的图象，得r=1，且a=1+，

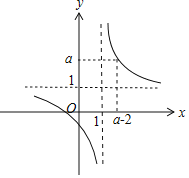
解得：a=2+；

②当0＜a＜1时，∵函数f（x）的值域是（1，+∞），即y＞1，

∴u=1+（r＜x＜a-2）的值域为（0，a），

作出函数u=1+（r＜x＜a-2）的图象，得a-2=-1，解得：a=1，矛盾．

综上，r=1，a=2+．