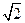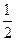题目内容
设数列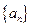 的前
的前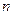 项的和
项的和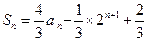 ,
,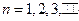
(Ⅰ)求首项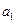 与通项
与通项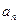 ;
;
(Ⅱ)设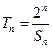 ,
,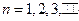 ,证明:
,证明: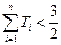 .
.
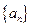 的前
的前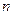 项的和
项的和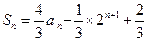 ,
,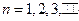
(Ⅰ)求首项
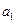 与通项
与通项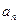 ;
;(Ⅱ)设
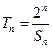 ,
,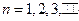 ,证明:
,证明: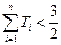 .
.(Ⅰ)a1=2,an=4n-2n, n="1,2,3," …,;(Ⅱ)同解析;
(Ⅰ)由 Sn=an-×2n+1+, n=1,2,3,… , ①
得 a1=S1= a1-×4+所以a1=2.
再由①有 Sn-1=an-1-×2n+, n=2,3,4,…
将①和②相减得: an=Sn-Sn-1= (an-an-1)-×(2n+1-2n),n="2,3," …
整理得: an+2n=4(an-1+2n-1),n="2,3," … ,
因而数列{ an+2n}是首项为a1+2=4,公比为4的等比数列,
即 : an+2n=4×4n-1= 4n, n="1,2,3," …,
因而an=4n-2n, n="1,2,3," …,
(Ⅱ)将an=4n-2n代入①得:
Sn= ×(4n-2n)-×2n+1 + = ×(2n+1-1)(2n+1-2)
= ×(2n+1-1)(2n-1)
Tn= = × = ×(- )
所以,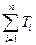 =
= 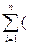 - )
- )
= ×(- ) <
得 a1=S1= a1-×4+所以a1=2.
再由①有 Sn-1=an-1-×2n+, n=2,3,4,…
将①和②相减得: an=Sn-Sn-1= (an-an-1)-×(2n+1-2n),n="2,3," …
整理得: an+2n=4(an-1+2n-1),n="2,3," … ,
因而数列{ an+2n}是首项为a1+2=4,公比为4的等比数列,
即 : an+2n=4×4n-1= 4n, n="1,2,3," …,
因而an=4n-2n, n="1,2,3," …,
(Ⅱ)将an=4n-2n代入①得:
Sn= ×(4n-2n)-×2n+1 + = ×(2n+1-1)(2n+1-2)
= ×(2n+1-1)(2n-1)
Tn= = × = ×(- )
所以,
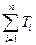 =
= 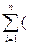 - )
- ) = ×(- ) <

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
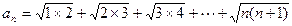
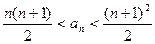
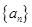 的前
的前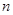 项和为
项和为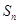 ,且
,且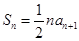 (
(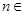 N*),其中
N*),其中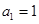 .
.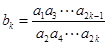 (
(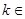 N*).
N*).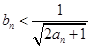 ;
;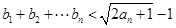 .
.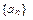 满足
满足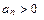 ,且对一切
,且对一切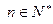 有
有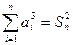 ,其中
,其中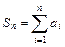 ,
, 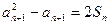 ,并求数列
,并求数列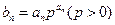 ,求数列
,求数列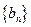 的前
的前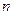 项和
项和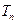 ;
;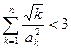 .
. 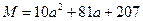 ,
,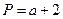 ,Q=
,Q=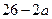 ;若将
;若将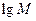 ,
,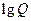 ,
,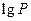 适当排序后可构成公差为1的等差数列
适当排序后可构成公差为1的等差数列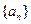 的前三项
的前三项 (I)在使得
(I)在使得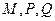 的大小;
的大小;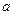 的值及数列
的值及数列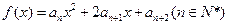 的图象在
的图象在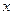 轴上截得的线段长为
轴上截得的线段长为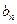 ,设
,设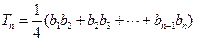 ,求
,求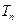 .
.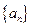 满足
满足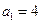 ,点
,点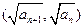 在直线
在直线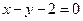 上,
上,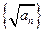 是等差数列;(2)求数列
是等差数列;(2)求数列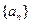 是等差数列,
是等差数列,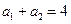 ,
,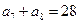 ,则该数列前10项和
,则该数列前10项和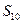 等于( )
等于( )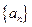 满足
满足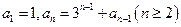 ,试写出
,试写出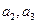 , 并求数列
, 并求数列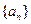 是公差不为0的等差数列,且
是公差不为0的等差数列,且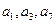 为等比数列
为等比数列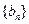 的连续三项,则数列
的连续三项,则数列