题目内容
(本题满分14分)
已知数列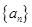 的前
的前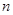 项和为
项和为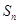 ,且
,且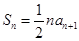 (
(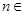 N*),其中
N*),其中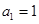 .
.
(Ⅰ)求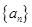 的通项公式;
的通项公式;
(Ⅱ) 设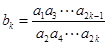 (
(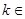 N*).
N*).
①证明: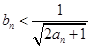 ;
;
② 求证: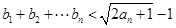 .
.
已知数列
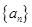 的前
的前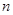 项和为
项和为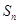 ,且
,且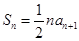 (
(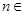 N*),其中
N*),其中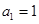 .
.(Ⅰ)求
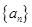 的通项公式;
的通项公式;(Ⅱ) 设
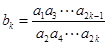 (
(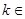 N*).
N*).①证明:
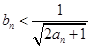 ;
;② 求证:
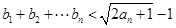 .
.(Ⅰ) n(Ⅱ)见解析
(Ⅰ)当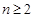 时,由
时,由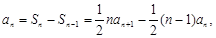 得
得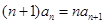 . 2分
. 2分
若存在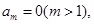 由
由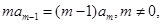 得
得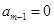 ,
,
从而有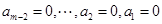 ,与
,与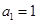 矛盾,所以
矛盾,所以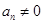 .
.
从而由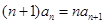 得
得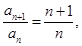 得
得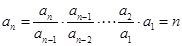 . 6分
. 6分
(Ⅱ)①证明: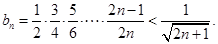
证法一:∵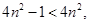 ∴
∴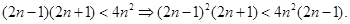
∴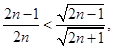
∴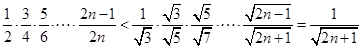 . 10分
. 10分
证法二: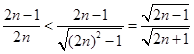 ,下同证法一. 10分
,下同证法一. 10分
证法三:(利用对偶式)设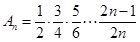 ,
,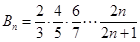 ,
,
则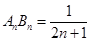 .又
.又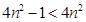 ,也即
,也即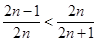 ,所以
,所以 ,也即
,也即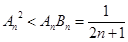 ,
,
又因为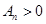 ,所以
,所以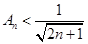 .即
.即
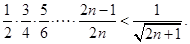 10分
10分
证法四:(数学归纳法)①当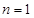 时,
时, 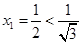 ,命题成立;
,命题成立;
②假设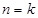 时,命题成立,即
时,命题成立,即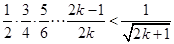 ,
,
则当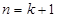 时,
时,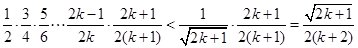
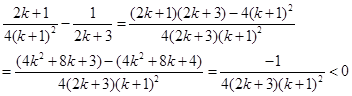
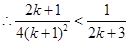 即
即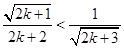
即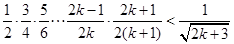
故当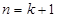 时,命题成立.
时,命题成立.
综上可知,对一切非零自然数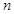 ,不等式②成立. 10分
,不等式②成立. 10分
②由于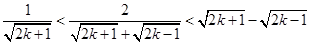 ,
,
所以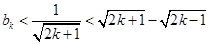 ,
,
从而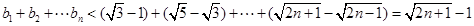 .
.
也即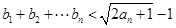 14分
14分
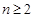 时,由
时,由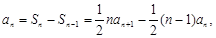 得
得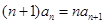 . 2分
. 2分若存在
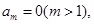 由
由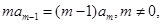 得
得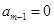 ,
,从而有
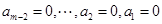 ,与
,与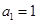 矛盾,所以
矛盾,所以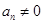 .
.从而由
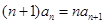 得
得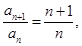 得
得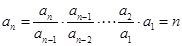 . 6分
. 6分(Ⅱ)①证明:
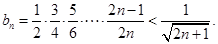
证法一:∵
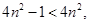 ∴
∴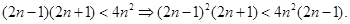
∴
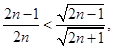
∴
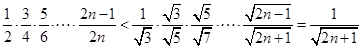 . 10分
. 10分证法二:
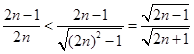 ,下同证法一. 10分
,下同证法一. 10分证法三:(利用对偶式)设
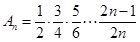 ,
,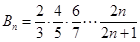 ,
,则
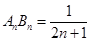 .又
.又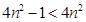 ,也即
,也即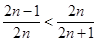 ,所以
,所以 ,也即
,也即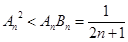 ,
,又因为
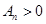 ,所以
,所以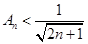 .即
.即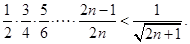 10分
10分证法四:(数学归纳法)①当
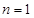 时,
时, 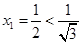 ,命题成立;
,命题成立;②假设
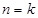 时,命题成立,即
时,命题成立,即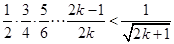 ,
,则当
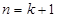 时,
时,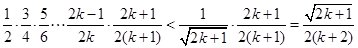
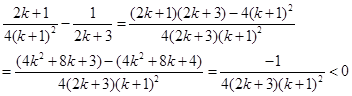
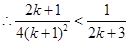 即
即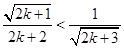
即
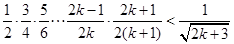
故当
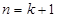 时,命题成立.
时,命题成立.综上可知,对一切非零自然数
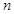 ,不等式②成立. 10分
,不等式②成立. 10分②由于
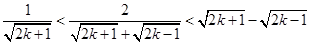 ,
,所以
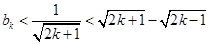 ,
,从而
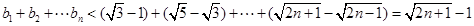 .
.也即
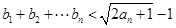 14分
14分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
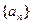 ,
,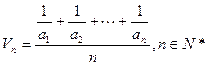 。
。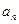 }的倒均数是
}的倒均数是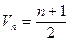 ,求数列{
,求数列{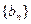 的首项为-1,公比为
的首项为-1,公比为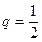 ,其倒数均为
,其倒数均为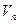 ,若存在正整数k,使得当
,若存在正整数k,使得当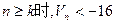 恒成立,试找出一个这样的k值(只需找出一个即可,不必证明)
恒成立,试找出一个这样的k值(只需找出一个即可,不必证明)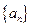 的前
的前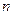 项的和
项的和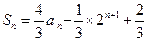 ,
,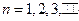
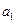 与通项
与通项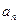 ;
;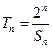 ,
,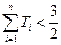 .
.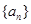 在中,
在中,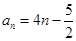 ,
,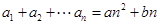 ,
,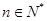 ,其中
,其中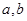 为常数,则
为常数,则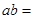
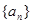 中,若
中,若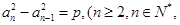
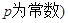 ,则称
,则称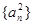 是等差数列;
是等差数列;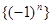 是等方差数列;
是等方差数列;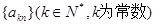 也是等方差数列;
也是等方差数列;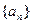 成等差数列,
成等差数列,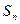 表示它的前
表示它的前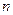 项和,且
项和,且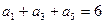 ,
,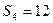 .
.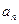 ;
;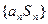 中,从第几项开始(含此项)以后各项均为负数?
中,从第几项开始(含此项)以后各项均为负数?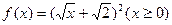 ,数列
,数列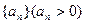 的前
的前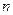 项和
项和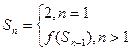
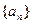 的通项公式;
的通项公式;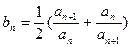 ,
,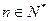 ,求
,求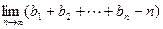 的值.
的值.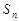 是等差数列
是等差数列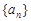 的前
的前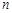 项和,若
项和,若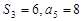 ,则
,则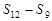 的值是( )
的值是( )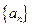 中,
中,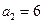 ,
,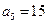 ,若
,若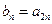 ,则数列
,则数列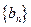 的前10项和
的前10项和 等于
等于