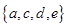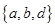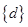题目内容
设不等式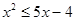 的解集为
的解集为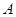 .
.
(1)求集合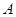 ;
;
(2)设关于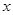 的不等式
的不等式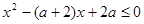 的解集为
的解集为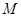 ,若
,若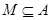 ,求实数
,求实数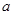 的取值范围.
的取值范围.
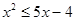 的解集为
的解集为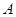 .
.(1)求集合
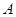 ;
;(2)设关于
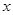 的不等式
的不等式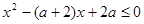 的解集为
的解集为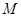 ,若
,若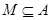 ,求实数
,求实数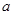 的取值范围.
的取值范围.(1)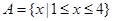 (2)
(2)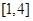 .
.
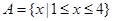 (2)
(2)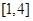 .
.试题分析:(1)解一元二次不等式,首先将一元二次不等式整理成二次项系数为正的情形,然后求对应一元二次方程的根,最后根据根的情况及不等式类型写出解集. 由
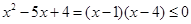 ,得
,得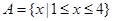 ,(2)对含参数的不等式,首先观察能否因式分解,这是简便解答的前提,然后根据根的大小讨论解集情况. 不等式等价于
,(2)对含参数的不等式,首先观察能否因式分解,这是简便解答的前提,然后根据根的大小讨论解集情况. 不等式等价于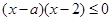 ,若
,若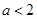 ,则
,则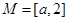 ,要
,要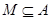 ,只需
,只需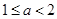 ,若
,若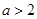 ,则
,则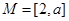 ,要
,要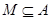 ,只需
,只需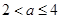 ,若
,若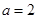 ,则
,则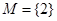 ,符合
,符合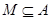 ,综上所述,
,综上所述,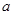 的取值范围为
的取值范围为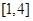 .
.解:
(1)
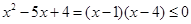 ,所以
,所以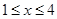 3分
3分所以不等式的解集
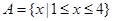 4分
4分(2)不等式等价于
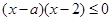 5分
5分若
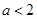 ,则
,则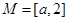 ,要
,要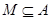 ,只需
,只需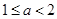 7分
7分若
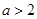 ,则
,则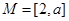 ,要
,要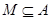 ,只需
,只需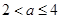 9分
9分若
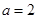 ,则
,则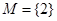 ,符合
,符合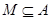 11分
11分综上所述,
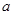 的取值范围为
的取值范围为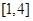 . 12分
. 12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
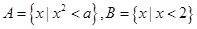 ,若
,若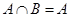 ,则实数
,则实数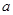 的取值范围是_______.
的取值范围是_______.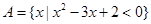 ,
,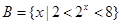 ,则( )
,则( )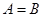
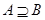

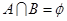
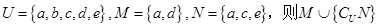 为
为