题目内容
【题目】已知函数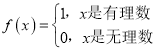 ,则下列判断中是真命题的有( ).
,则下列判断中是真命题的有( ).
①![]() ,
,![]() ;②
;②![]() 是偶函数;③对于任意一个非零有理数
是偶函数;③对于任意一个非零有理数![]() ,
,![]() ,
,![]() ;④存在三个点
;④存在三个点![]() ,
,![]() ,
,![]() ,使得
,使得![]() 为等边三角形.
为等边三角形.
A.①②③B.①②③④C.①③④D.②③④
【答案】B
【解析】
①根据函数的对应法则,可知无论x是有理数还是无理数,均有f(f(x))=1;
②根据函数奇偶性的定义,可得f(x)是偶函数;
③根据函数的表达式,结合有理数和无理数的性质;
④取x1=![]() ,x2=0,x3=
,x2=0,x3=![]() ,可得
,可得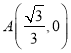 ,
,![]() ,
,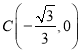 ,三点恰好构成等边三角形.
,三点恰好构成等边三角形.
①∵当x为有理数时,f(x)=1;当x为无理数时,f(x)=0,
∴当x为有理数时,![]() =f(1)=1;当x为无理数时,
=f(1)=1;当x为无理数时,![]() =f(0)=1,
=f(0)=1,
即无论x是有理数还是无理数,均有![]() =1,故①正确;
=1,故①正确;
②∵有理数的相反数还是有理数,无理数的相反数还是无理数,
∴对任意x∈R,都有![]() ,故②正确;
,故②正确;
③若x是有理数,则x+T也是有理数; 若x是无理数,则x+T也是无理数,
∴根据函数的表达式,任取一个不为零的有理数T,![]() 对x∈R恒成立,故③正确;
对x∈R恒成立,故③正确;
④取x1=![]() ,x2=0,x3=
,x2=0,x3=![]() ,可得
,可得![]() ,
,
∴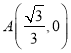 ,
,![]() ,
,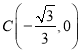 ,恰好△ABC为等边三角形,故④正确.
,恰好△ABC为等边三角形,故④正确.
即真命题的个数是4个,
故选:B.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目