题目内容
【题目】已知函数f(x)= ![]() ﹣
﹣ ![]() .
.
(1)判断f(x)的奇偶性;
(2)判断f(x)的单调性,并用定义证明;
(3)解不等式f(f(x))+f( ![]() )<0.
)<0.
【答案】
(1)解:由2x+1>1得函数的定义域为R,
又f(﹣x)+f(x)= ![]() ﹣
﹣ ![]() +
+ ![]() ﹣
﹣ ![]() =
= ![]() +
+ ![]() ﹣1=1﹣1=0.
﹣1=1﹣1=0.
则f(﹣x)=﹣f(x),
故f(x)为奇函数
(2)解:f(x)为R上的减函数
证明如下:
任取x1<x2,则f(x1)﹣f(x2)= ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() +
+ ![]() =
= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∵x1<x2,∴ ![]() <
< ![]() ,
,
则f(x1)﹣f(x2)= ![]() >0,
>0,
∴f(x1)>f(x2),
故f(x)为R上的减函数
(3)解:由(1)(2)知f(x)在R上是奇函数且单调递减,
由f(f(x))+f( ![]() )<0得f(f(x))<﹣f(
)<0得f(f(x))<﹣f( ![]() )=f(﹣
)=f(﹣ ![]() ),
),
则f(x)>﹣ ![]() ,
,
∴ ![]() ﹣
﹣ ![]() >﹣
>﹣ ![]() ,
,
即2x<7,得x<log27,
故不等式的解集为(﹣∞,log27)
【解析】(1)根据函数奇偶性的定义进行判断即可,(2)根据函数单调性的定义,利用定义法进行证明,(3)根据函数奇偶性和单调性之间的关系将不等式进行转化求解即可.
【考点精析】根据题目的已知条件,利用函数单调性的判断方法和函数的奇偶性的相关知识可以得到问题的答案,需要掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;偶函数的图象关于y轴对称;奇函数的图象关于原点对称.

【题目】某学校的特长班有50名学生,其中有体育生20名,艺术生30名,在学校组织的一次体检中,该班所有学生进行了心率测试,心率全部介于50次/分到75次/分之间,现将数据分成五组,第一组![]() ,第二组
,第二组![]() ,…,第五组
,…,第五组![]() ,按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为
,按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前三组的频率之比为![]() .
.
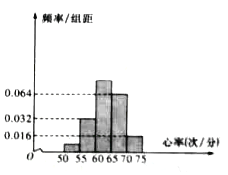
(Ⅰ)求![]() 的值,并求这50名同学心率的平均值;
的值,并求这50名同学心率的平均值;
(Ⅱ)因为学习专业的原因,体育生常年进行系统的身体锻炼,艺术生则很少进行系统的身体锻炼,若从第一组和第二组的学生中随机抽取一名,该学生是体育生的概率为0.8,请将下面的列联表补充完整,并判断是否有99.5%的把握认为心率小于60次/分与常年进行系统的身体锻炼有关?说明你的理由.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: 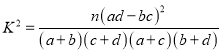 ,其中
,其中![]()
心率小于60次/分 | 心率不小于60次/分 | 合计 | |
体育生 | 20 | ||
艺术生 | 30 | ||
合计 | 50 |
【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.某市场研究人员为了了解共享单车运营公司M的经营状况,对该公司最近六个月内的市场占有率进行了统计,并绘制了相应的折线图.
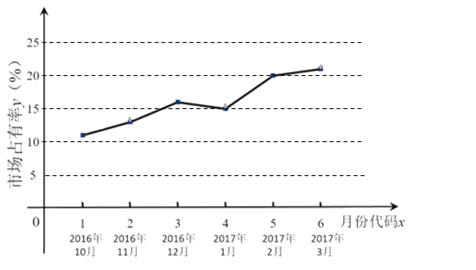
(Ⅰ)由折线图可以看出,可用线性回归模型拟合月度市场占有率y与月份代码x之间的关系.求y关于x的线性回归方程,并预测M公司2017年4月份(即x=7时)的市场占有率;
(Ⅱ)为进一步扩大市场,公司拟再采购一批单车.现有采购成本分别为1000元/辆和1200元/辆的A、B两款车型可供选择,按规定每辆单车最多使用4年,但由于多种原因(如骑行频率等)会导致车辆报废年限各不相同.考虑到公司运营的经济效益,该公司决定先对两款车型的单车各100辆进行科学模拟测试,得到两款单车使用寿命频数表如下:
车型 | 1年 | 2年 | 3年 | 4年 | 总计 |
A | 20 | 35 | 35 | 10 | 100 |
B | 10 | 30 | 40 | 20 | 100 |
经测算,平均每辆单车每年可以带来收入500元.不考虑除采购成本之外的其他成本,假设每辆单车的使用寿命都是整数年,且以频率作为每辆单车使用寿命的概率.如果你是M公司的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型?
参考数据: ![]()
![]()
(参考公式:回归直线方程为![]() ,其中
,其中 )
)
【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.某市场研究人员为了了解共享单车运营公司M的经营状况,对该公司最近六个月内的市场占有率进行了统计,并绘制了相应的折线图.
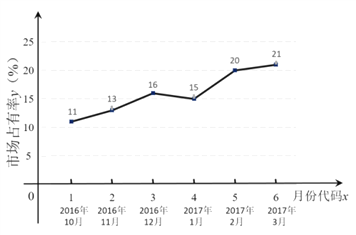
(Ⅰ)由折线图可以看出,可用线性回归模型拟合月度市场占有率y与月份代码x之间的关系.求y关于x的线性回归方程,并预测M公司2017年4月份的市场占有率;
(Ⅱ)为进一步扩大市场,公司拟再采购一批单车.现有采购成本分别为1000元/辆和1200元/辆的A、B两款车型可供选择,按规定每辆单车最多使用4年,但由于多种原因(如骑行频率等)会导致车辆报废年限各不相同.考虑到公司运营的经济效益,该公司决定先对两款车型的单车各100辆进行科学模拟测试,得到两款单车使用寿命频数表如下:
车型 | 1年 | 2年 | 3年 | 4年 | 总计 |
A | 20 | 35 | 35 | 10 | 100 |
B | 10 | 30 | 40 | 20 | 100 |
经测算,平均每辆单车每年可以带来收入500元.不考虑除采购成本之外的其他成本,假设每辆单车的使用寿命都是整数年,且以频率作为每辆单车使用寿命的概率.如果你是M公司的负责人,以每辆单车产生利润的期望值为决策依据,你会选择采购哪款车型?
参考数据: ![]() ,
, ![]() .
.
参考公式:
回归直线方程为![]() 其中
其中
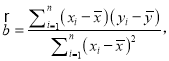
![]()