题目内容
设有一张边长为48cm的正方形铁皮 ,从其四个角各截去一个大小相同的小正方形 ,然后将剩余部分折成一个无盖的长方体盒子 ,所得盒子的体积V是关于截去的小正方形的边长x的函数 .
(1)随着x的变化 ,盒子体积V是如何变化的?
(2)截去的小正方形的边长x为多少时 ,盒子的体积最大?最大体积是多少?
(1)随着x的变化 ,盒子体积V是如何变化的?
(2)截去的小正方形的边长x为多少时 ,盒子的体积最大?最大体积是多少?
(1)V = x ,定义域为0 <x<24
,定义域为0 <x<24
(2)当截取的小正方形的边长为8cm时 ,得到的盒子体积最大 ,且最大体积为8192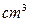
 ,定义域为0 <x<24
,定义域为0 <x<24(2)当截取的小正方形的边长为8cm时 ,得到的盒子体积最大 ,且最大体积为8192
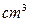
解 :(1)有题意可得V关于x的函数解析式为
V = x ,
,
定义域为0 <x<24 ,
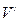 =
=  -4 x
-4 x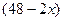 = 12(x-8)(x-24),
= 12(x-8)(x-24),
当x∈(0 ,8)时体积V单调递增 ,x∈(8 ,24)时体积V单调递减 ;
(2)由(1)知 ,x = 8时 ,体积V有极大值 ,且唯一 ,那么x = 8时体积V有最大值 ,
最大值 =" V(8)" = 8192(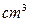 ),
),
即当截取的小正方形的边长为8cm时 ,得到的盒子体积最大 ,且最大体积为8192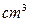 .
.
V = x
 ,
,定义域为0 <x<24 ,
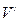 =
=  -4 x
-4 x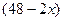 = 12(x-8)(x-24),
= 12(x-8)(x-24),当x∈(0 ,8)时体积V单调递增 ,x∈(8 ,24)时体积V单调递减 ;
(2)由(1)知 ,x = 8时 ,体积V有极大值 ,且唯一 ,那么x = 8时体积V有最大值 ,
最大值 =" V(8)" = 8192(
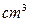 ),
),即当截取的小正方形的边长为8cm时 ,得到的盒子体积最大 ,且最大体积为8192
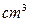 .
.
练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
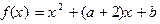 满足
满足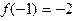 ;
;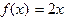 有唯一的解,求实数
有唯一的解,求实数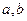 的值;
的值;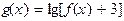 的定义域为R,求实数
的定义域为R,求实数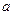 的取值范围.
的取值范围.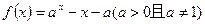 有两个零点,则实数
有两个零点,则实数 的取值范围是
的取值范围是  的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度
的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度 不得
不得 超过
超过 米,房屋正面的造价为400元
米,房屋正面的造价为400元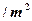 ,房屋侧面的造价为150元
,房屋侧面的造价为150元 表示成
表示成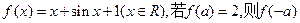 的值为 。
的值为 。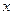

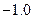
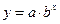
 ,则从集合A到集合B的不同映射共有 个。
,则从集合A到集合B的不同映射共有 个。 ②
②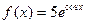 ;③
;③ ;④
;④ 。
。 定义域内的任意一个自变量
定义域内的任意一个自变量 ,都存在唯一的自变量
,都存在唯一的自变量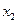 ,使
,使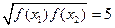 成立的函数为 ( )
成立的函数为 ( )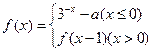 若关于x的方程
若关于x的方程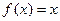 有且仅有二个
有且仅有二个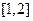
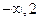 )
)