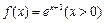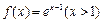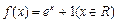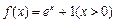题目内容
集合M={a,b,c},N={-1,0,1},映射f:M→N满足f(a)+f(b)+f(c)=0,那么映射f:M→N的个数是多少?
∵f(a)∈N,f(b)∈N,f(c)∈N,且
f(a)+f(b)+f(c)=0,
∴有0+0+0=0+1+(-1)=0.当f(a)=f(b)=f(c)=0时,只有一个映射;当f(a)、f(b)、f(c)中恰有一个为0,而另两个分别为1,-1时,有C·A=6个映射.因此所求的映射的个数为1+6=7.
f(a)+f(b)+f(c)=0,
∴有0+0+0=0+1+(-1)=0.当f(a)=f(b)=f(c)=0时,只有一个映射;当f(a)、f(b)、f(c)中恰有一个为0,而另两个分别为1,-1时,有C·A=6个映射.因此所求的映射的个数为1+6=7.
略

练习册系列答案
相关题目
 (本小题満分14分)
(本小题満分14分) 的图象与
的图象与 轴所围成的封闭图形的面积为
轴所围成的封闭图形的面积为 ,则
,则 的展开式中常数项为
的展开式中常数项为 


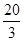
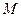 是满足下列性质的函数
是满足下列性质的函数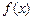 的全体:存在非零常数k, 对定义域中
的全体:存在非零常数k, 对定义域中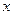 ,等式
,等式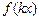 =
=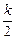 +
+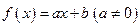 ,
,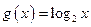 ,则函数
,则函数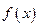 、
、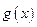 与集合
与集合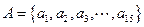 与
与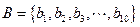 ,若从
,若从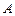 到
到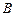 的映射
的映射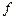 使
使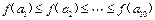
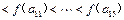 ,则这样的映射共有( )
,则这样的映射共有( )
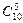 个
个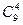 个
个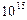 个
个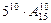 个
个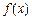 的图象与函数
的图象与函数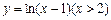 的图象关于直线
的图象关于直线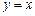 对称,则
对称,则