题目内容
 (本小题満分14分)
(本小题満分14分)二次函数f(x+1)-f(x)=2x,且f(0)=1
(1)求f(x)的解析式;
(2)在区间[-1,1]上,y= f(x)的图像恒在y=2x+m的图像上方,试确定实数m的取值范围。
方法一
(1)令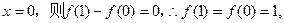
∴二次函数图像的 对称轴为
对称轴为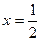 。
。
∴可令二次函数的解析式为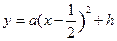
由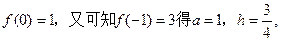
∴二次函数的解析式为
(2)∵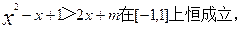
∴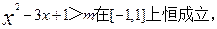
令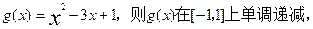
∴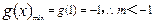
方法二
解:设f(x)="ax^2+bx+c"
∵f(0)="1"
∴c="1"
∴f(x)="ax^2+bx+1"
∴f(x+1)="a(x+1)^2+b(x+1)+1=ax^2+(2a+b)x+a+b+1"
∴f(x+1)-f(x)="ax^2+(2a+b)x+a+b+1-ax^2-bx-1=2ax+a+b"
∵f(x+1)-f(x)="2x"
∴2ax+a+b="2x"
∴2a=2且a+b="0"
∴a="1,b=-1"
∴f(x)=x^2-x+1
(1)令
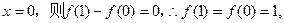
∴二次函数图像的
 对称轴为
对称轴为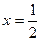 。
。∴可令二次函数的解析式为
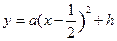
由
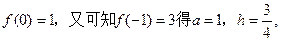
∴二次函数的解析式为

(2)∵
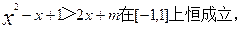
∴
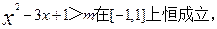
令
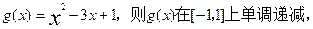
∴
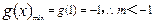
方法二
解:设f(x)="ax^2+bx+c"
∵f(0)="1"
∴c="1"
∴f(x)="ax^2+bx+1"
∴f(x+1)="a(x+1)^2+b(x+1)+1=ax^2+(2a+b)x+a+b+1"
∴f(x+1)-f(x)="ax^2+(2a+b)x+a+b+1-ax^2-bx-1=2ax+a+b"
∵f(x+1)-f(x)="2x"
∴2ax+a+b="2x"
∴2a=2且a+b="0"
∴a="1,b=-1"
∴f(x)=x^2-x+1
略

练习册系列答案
相关题目
 的定义域为集合
的定义域为集合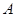 ,函数
,函数 的定义域为集合
的定义域为集合 ,则
,则




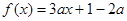 ,在区间
,在区间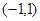 上存在一个零点,则
上存在一个零点,则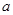 的取值范围是
的取值范围是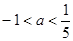
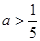
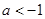
 ,
, ,
,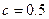 ,则它们的大小关系是
,则它们的大小关系是

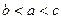


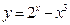 的图象大致是
的图象大致是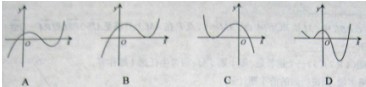
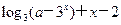 ,若f(x)存在零点,则实数a的取值范围
,若f(x)存在零点,则实数a的取值范围