Question

【题目】斜率为2的直线l在双曲线上截得的弦长为，求l的方程．

Answer 1

【答案】y＝2x±

【解析】

设直线的方程为,设和双曲线的两交点为，将直线方程代入双曲线方程可得到关于的一元二次方程，根据韦达定理可用表示,然后求弦长等于 ,这样可得到关于的方程，解方程即得的值，从而便求出来直线的方程.

设直线l的方程为y＝2x＋m，

由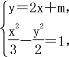得10x2＋12mx＋3(m2＋2)＝0.(*)

设直线l与双曲线交于A(x1，y1)，B(x2，y2)两点，由根与系数的关系，

得x1＋x2＝－m，x1x2＝ (m2＋2)．

∴|AB|2＝(x1－x2)2＋(y1－y2)2＝5(x1－x2)2＝5[(x1＋x2)2－4x1x2]＝5.∵|AB|＝，∴m2－6(m2＋2)＝6，∴m2＝15，m＝±.

由(*)式得Δ＝24m2－240，

把m＝±代入上式，得Δ>0，∴m的值为±，

∴所求l的方程为y＝2x±.