题目内容
【题目】已知动点M（x，y）到直线ι：x=4的距离是它到点N（1，0）的距离的2倍．
（1）求动点M的轨迹C的方程；
（2）过点P（0，3）的直线m与轨迹C交于A，B两点，若A是PB的中点，求点A的坐标．
【答案】
（1）解：点M（x，y）到直线x=4的距离是它到点N（1，0）的距离的2倍，
则|x﹣4|=2 
，即（x﹣4）2=4（x﹣1）2+4y2，整理得 
，
所以，动点M的轨迹是椭圆，方程为
（2）解：P（0，3），设A（x1，y1），B（x2，y2），
由A是PB的中点，得2x1=x2，椭圆的上下顶点坐标分别是（0，3）和（0，﹣3），
经检验直线m不经过这两点，即直线m的斜率k存在，
设直线m的方程为y=kx+3，联立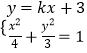 
，得 
，
所以 
，得 
，
设直线m的方程为 
，则 
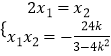，得 
【解析】（1）由已知得|x﹣4|=2 ，由此能求出动点M的轨迹方程．（2）P（0，3），设A（x1 ， y1），B（x2 ， y2），由A是PB的中点，得2x1=x2 ， 设直线m的方程为y=kx+3，代入椭圆，得（3+4k2）x2+24kx+24=0，由此能求出点A的坐标．
练习册系列答案
相关题目
