题目内容
【题目】已知命题p:函数f(x)=|2x+3c|在[-1,+∞)上单调递增;命题q:函数g(x)=![]() +2有零点.
+2有零点.
(1)若命题p和q均为真命题,求实数c的取值范围;
(2)是否存在实数c,使得p∧(q)是真命题?若存在,求出c的取值范围;若不存在,说明理由.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)将f(x)转化成分段函数的形式,易得出f(x)的递增区间,结合[-1,+∞)上单调递增,再结合g(x)=0有解,求得c的取值范围.
(2) 使p∧ (q)是真命题,应使p真q假,得不等式组,解得c的取值范围.
因为f(x)=|2x+3c|=
所以f(x)的单调递增区间是![]() .
.
又因为f(x)在[-1,+∞)上单调递增,
所以-![]() ≤-1,解得c≥
≤-1,解得c≥![]() .
.
因为函数g(x)=![]() +2有零点,
+2有零点,
所以方程![]() +2=0有实数根,
+2=0有实数根,
即2x2+cx+2=0有实数根,
所以c2-16≥0,解得c≥4或c≤-4.
(1)当命题p和q均为真命题时,
应有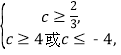 即c≥4.
即c≥4.
故c的取值范围是[4,+∞).
(2)要使p∧ (q)是真命题,应使p真q假,
因此有
解得![]() ≤c<4,
≤c<4,
故存在实数c,使得p∧ (q)是真命题,其取值范围是![]() .
.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目

