题目内容
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,短轴的一个端点为
,短轴的一个端点为![]() .过椭圆左顶点
.过椭圆左顶点![]() 的直线
的直线![]() 与椭圆的另一交点为
与椭圆的另一交点为![]() .
.
(1)求椭圆的方程;
(2)若![]() 与直线
与直线![]() 交于点
交于点![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】试题分析:(1)根据条件可得![]() ,
,![]() ,再结合条件
,再结合条件![]() ,计算得到
,计算得到![]() ,
,![]() 和
和![]() ,求得椭圆的标准方程;(2)首先设
,求得椭圆的标准方程;(2)首先设![]() ,根据点
,根据点![]() 的坐标求出直线
的坐标求出直线![]() 的方程,并计算得到点
的方程,并计算得到点![]() 的坐标,并表示
的坐标,并表示![]() ,最后根据点
,最后根据点![]() 在椭圆上,满足椭圆方程
在椭圆上,满足椭圆方程![]() ,计算得到常数;(3)设直线方程
,计算得到常数;(3)设直线方程![]() 与椭圆方程联立,根据弦长公式
与椭圆方程联立,根据弦长公式![]() ,解得直线的斜率,最后得到直线的倾斜角.
,解得直线的斜率,最后得到直线的倾斜角.
试题解析:(1)∵![]()
∴![]()
∴椭圆的方程为![]()
(2)由(1)可知点![]() ,设
,设![]() ,则
,则![]()
令![]() ,解得
,解得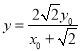 ,既
,既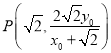
∴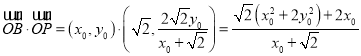
又∵![]() 在椭圆上,则
在椭圆上,则![]() ,
,
∴![]()
(3)当直线![]() 的斜率不存在时,不符合题意;当直线
的斜率不存在时,不符合题意;当直线![]() 的斜率存在时,设其为
的斜率存在时,设其为![]() ,则
,则![]()
由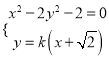 可得,
可得, ![]()
由于![]() ,则设
,则设![]() 可得,
可得, ![]() ,
, ![]()
∴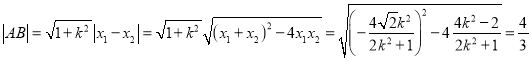
∴解得![]()
∴直线![]() 的倾斜角为
的倾斜角为![]() 或
或![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目