题目内容
已知关于x的实系数方程x2+ax+2b=0的一根在(0,1)内,另一根在(1,2)内,则点(a,b)所在区域的面积为
.
| 1 |
| 2 |
| 1 |
| 2 |
分析:由方程x2+ax+2b=0的一根在(0,1)内,另一根在(1,2)内,列式得到关于a、b的约束条件,然后作出可行域,
数形结合可以求得点(a,b)所在区域的面积.
数形结合可以求得点(a,b)所在区域的面积.
解答: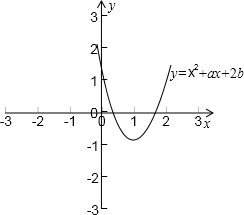 解:如图,令f(x)=x2+ax+2b,
解:如图,令f(x)=x2+ax+2b,
要使关于x的实系数方程x2+ax+2b=0的一根在(0,1)内,另一根在(1,2)内,
则
,即
作可行域如图,
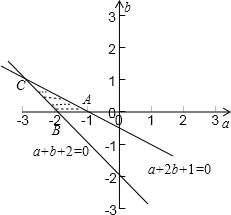
由
,得:C(-3,1)
所以点(a,b)所在区域的面积为S=
×1×1=
.
故答案为
.
 解:如图,令f(x)=x2+ax+2b,
解:如图,令f(x)=x2+ax+2b,要使关于x的实系数方程x2+ax+2b=0的一根在(0,1)内,另一根在(1,2)内,
则
|
|
作可行域如图,

由
|
所以点(a,b)所在区域的面积为S=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为
| 1 |
| 2 |
点评:本题考查了二元一次不等式(组)与平面区域,考查了一元二次方程的根的分布与系数之间的关系,考查了数形结合的解题思想,灵活运用三个二次的结合是解答此题的关键,此题是中档题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目