题目内容
下列命题
①关于x，y二元一次方程组
的系数行列式D=0是该方程组有解的必要非充分条件；
②已知E，F，G，H是空间四点，命题甲：E，F，G，H四点不共面，命题乙：直线EF和GH不相交，则甲是乙成立的充分不必要条件；
③“a＜2”是“对任意的实数x，|x+1|+|x-1|≥a恒成立”的充要条件；
④“p=0或p=4”是“关于x的实系数方程
=x+p有且仅有一个实数根”的非充分非必要条件．
其中为真命题的序号是
①关于x，y二元一次方程组
|
②已知E，F，G，H是空间四点，命题甲：E，F，G，H四点不共面，命题乙：直线EF和GH不相交，则甲是乙成立的充分不必要条件；
③“a＜2”是“对任意的实数x，|x+1|+|x-1|≥a恒成立”的充要条件；
④“p=0或p=4”是“关于x的实系数方程
| p |
| x |
其中为真命题的序号是
②④
②④
．分析：①系数行列式D≠0，关于x，y二元一次方程组
有唯一解，系数行列式D=0，Dx≠0或Dy≠0，关于x，y二元一次方程组
无解，系数行列式D=0，Dx=Dy=0 ，关于x，y二元一次方程组
有无穷组解；②已知E，F，G，H是空间四点，命题甲：E，F，G，H四点不共面，命题乙：直线EF和GH不相交，则甲⇒乙，乙推不出甲；③“a＜2”⇒“对任意的实数x，|x+1|+|x-1|≥a”，“对任意的实数x，|x+1|+|x-1|≥a”推不出“a＜2”；④“p=0或p=4”推不出“关于x的实系数方程
=x+p有且仅有一个实数根”，“关于x的实系数方程
=x+p有且仅有一个实数根”推不出“p=0或p=4”．
|
|
|
| p |
| x |
| p |
| x |
解答：解：①系数行列式D≠0，关于x，y二元一次方程组
有唯一解，
系数行列式D=0，Dx≠0或Dy≠0，关于x，y二元一次方程组
无解，
系数行列式D=0，Dx=Dy=0 ，关于x，y二元一次方程组
有无穷组解，
故关于x，y二元一次方程组
的系数行列式D=0是该方程组有解的非必要非充分条件．
故①不正确；
②已知E，F，G，H是空间四点，命题甲：E，F，G，H四点不共面，命题乙：直线EF和GH不相交，
则甲⇒乙，乙推不出甲，故②正确；
③设y=|x+1|+|x-1|，
由x+1=0，得x=-1；由x-1=0，得x=1．
当x≥1时，y=2x≥2；
当-1≤x＜1时，y=2；
当x＜-1时，y=-2x＞2．
故|x+1|+|x-1|≥2．
∴“a＜2”⇒“对任意的实数x，|x+1|+|x-1|≥a”，
“对任意的实数x，|x+1|+|x-1|≥a”推不出“a＜2”．
故“a＜2”是“对任意的实数x，|x+1|+|x-1|≥a恒成立”的充分不必要条件，
故③不成立；
④“p=0或p=4”推不出“关于x的实系数方程
=x+p有且仅有一个实数根”，
“关于x的实系数方程
=x+p有且仅有一个实数根”推不出“p=0或p=4”，
故④成立．
故答案为：②④．
|
系数行列式D=0，Dx≠0或Dy≠0，关于x，y二元一次方程组
|
系数行列式D=0，Dx=Dy=0 ，关于x，y二元一次方程组
|
故关于x，y二元一次方程组
|
故①不正确；
②已知E，F，G，H是空间四点，命题甲：E，F，G，H四点不共面，命题乙：直线EF和GH不相交，
则甲⇒乙，乙推不出甲，故②正确；
③设y=|x+1|+|x-1|，
由x+1=0，得x=-1；由x-1=0，得x=1．
当x≥1时，y=2x≥2；
当-1≤x＜1时，y=2；
当x＜-1时，y=-2x＞2．
故|x+1|+|x-1|≥2．
∴“a＜2”⇒“对任意的实数x，|x+1|+|x-1|≥a”，
“对任意的实数x，|x+1|+|x-1|≥a”推不出“a＜2”．
故“a＜2”是“对任意的实数x，|x+1|+|x-1|≥a恒成立”的充分不必要条件，
故③不成立；
④“p=0或p=4”推不出“关于x的实系数方程
| p |
| x |
“关于x的实系数方程
| p |
| x |
故④成立．
故答案为：②④．
点评：本题考查必要条件、充分条件、充要条件的性质和应用，是基础题．解题时要注意行列式、空间几何、不等式、方程等知识点的灵活运用．
练习册系列答案
相关题目
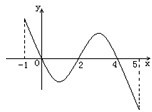已知函数f（x）的定义域为[-1，5]，部分对应值如下表，f（x）的导函数y=f′（x）的图象如图所示．给出关于f（x）的下列命题：
的系数行列式D=0是该方程组有解的必要非充分条件；
有且仅有一个实数根”的非充分非必要条件．