题目内容
设集合A={a|f(x)=8x3-3ax2+6x是(0,+∞)上的增函数},B=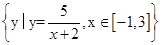
,则∁R(A∩B)= .
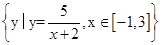,则∁R(A∩B)= .(-∞,1)∪(4,+∞)
f'(x)=24x2-6ax+6,要使函数在(0,+∞)上是增函数,则f'(x)=24x2-6ax+6≥0恒成立,即a≤4x+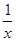
,因为4x+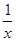≥2
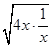=4,所以a≤4,即集合A={a|a≤4},集合B=
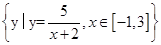={y|1≤y≤5},所以A∩B={x|1≤x≤4},所以∁R(A∩B)=(-∞,1)∪(4,+∞).
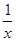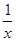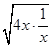,因为4x+≥2=4,所以a≤4,即集合A={a|a≤4},集合B=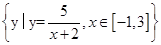={y|1≤y≤5},所以A∩B={x|1≤x≤4},所以∁R(A∩B)=(-∞,1)∪(4,+∞).
练习册系列答案
阅读快车系列答案
相关题目
B，求实数a的取值范围．
,则实数a的取值范围是( )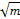
x+1=0},若A∩R=?,则实数m的取值范围是( )
，
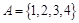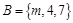，若
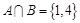，则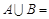
．