题目内容
在实数集R中定义一种运算“⊕”,具有性质:①对任意a,b∈R,a⊕b=b⊕a;
②对任意a∈R,a⊕0=a;
③对任意a,b,c∈R,(a⊕b)⊕c=c⊕(ab)+(a⊕c)+(b⊕c)-2c.
函数f(x)=x⊕
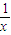 (x>0)的最小值为( )
(x>0)的最小值为( )A.4
B.3
C.2

D.1
【答案】分析:根据题中给出的对应法则,可得f(x)=(x⊕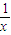 )⊕0=1+x+
)⊕0=1+x+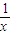 ,利用基本不等式求最值可得x+
,利用基本不等式求最值可得x+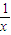 ≥2,当且仅当x=1时等号成立,由此可得函数f(x)的最小值为f(1)=3.
≥2,当且仅当x=1时等号成立,由此可得函数f(x)的最小值为f(1)=3.
解答:解:根据题意,得
f(x)=x⊕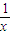 =(x⊕
=(x⊕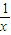 )⊕0=0⊕(x•
)⊕0=0⊕(x•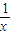 )+(x⊕0)+(
)+(x⊕0)+(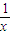 ⊕0 )-2×0=1+x+
⊕0 )-2×0=1+x+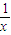
即f(x)=1+x+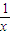
∵x>0,可得x+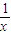 ≥2,当且仅当x=
≥2,当且仅当x=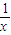 =1,即x=1时等号成立
=1,即x=1时等号成立
∴1+x+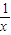 ≥2+1=3,可得函数f(x)=x⊕
≥2+1=3,可得函数f(x)=x⊕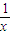 (x>0)的最小值为f(1)=3
(x>0)的最小值为f(1)=3
故选:B
点评:本题给出新定义,求函数f(x)的最小值.着重考查了利用基本不等式求最值、函数的解析式求法和简单的合情推理等知识,属于中档题.
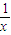 )⊕0=1+x+
)⊕0=1+x+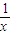 ,利用基本不等式求最值可得x+
,利用基本不等式求最值可得x+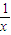 ≥2,当且仅当x=1时等号成立,由此可得函数f(x)的最小值为f(1)=3.
≥2,当且仅当x=1时等号成立,由此可得函数f(x)的最小值为f(1)=3.解答:解:根据题意,得
f(x)=x⊕
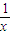 =(x⊕
=(x⊕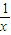 )⊕0=0⊕(x•
)⊕0=0⊕(x•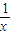 )+(x⊕0)+(
)+(x⊕0)+(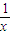 ⊕0 )-2×0=1+x+
⊕0 )-2×0=1+x+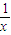
即f(x)=1+x+
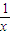
∵x>0,可得x+
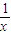 ≥2,当且仅当x=
≥2,当且仅当x=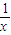 =1,即x=1时等号成立
=1,即x=1时等号成立∴1+x+
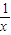 ≥2+1=3,可得函数f(x)=x⊕
≥2+1=3,可得函数f(x)=x⊕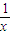 (x>0)的最小值为f(1)=3
(x>0)的最小值为f(1)=3故选:B
点评:本题给出新定义,求函数f(x)的最小值.着重考查了利用基本不等式求最值、函数的解析式求法和简单的合情推理等知识,属于中档题.

练习册系列答案
相关题目