题目内容
(本小题满分14分)等差数列
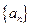 的首项与公差均大于零,
的首项与公差均大于零,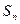 是数列
是数列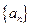 的前n项和,对于任意
的前n项和,对于任意
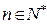 ,都有
,都有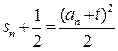 成立
成立(1)求数列
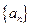 的公差和
的公差和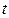 的值;
的值;(2)设
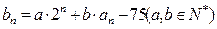 ,且数列
,且数列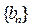 的前n项和
的前n项和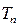 的最小值为
的最小值为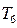 ,求
,求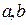 的值.
的值.(1)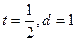 (2)
(2)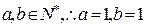
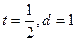 (2)
(2)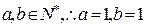
解、(1)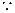
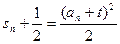 ┅┅①,
┅┅①,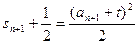 ┅┅ ②
┅┅ ② 
两式相减得: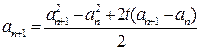
又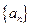 为等差数列,设公差为
为等差数列,设公差为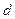 ,则这上式化为:
,则这上式化为: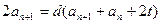
又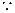
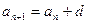 ,
,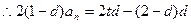 ,对任意的
,对任意的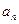 都成立,则
都成立,则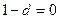 且
且
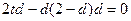 ,
,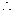
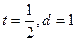 ┅┅┅┅┅┅┅┅┅┅7分
┅┅┅┅┅┅┅┅┅┅7分
(2)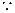
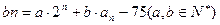 ,且等差数列
,且等差数列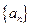 的通项为
的通项为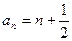 ,
,

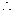 数列
数列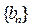 为递增数列。
为递增数列。
又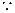 数列
数列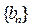 的前
的前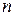 项和的最小值为
项和的最小值为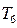 ,则有
,则有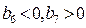
即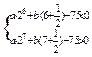 而
而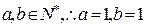 ┅┅┅┅┅┅┅┅┅┅14分
┅┅┅┅┅┅┅┅┅┅14分
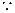
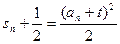 ┅┅①,
┅┅①,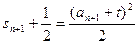 ┅┅ ②
┅┅ ② 
两式相减得:
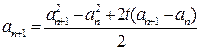
又
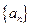 为等差数列,设公差为
为等差数列,设公差为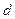 ,则这上式化为:
,则这上式化为: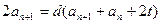
又
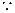
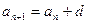 ,
,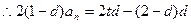 ,对任意的
,对任意的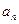 都成立,则
都成立,则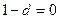 且
且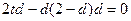 ,
,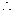
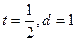 ┅┅┅┅┅┅┅┅┅┅7分
┅┅┅┅┅┅┅┅┅┅7分(2)
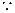
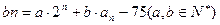 ,且等差数列
,且等差数列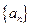 的通项为
的通项为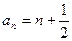 ,
,
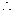 数列
数列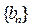 为递增数列。
为递增数列。又
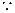 数列
数列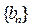 的前
的前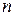 项和的最小值为
项和的最小值为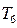 ,则有
,则有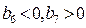
即
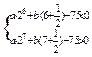 而
而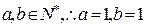 ┅┅┅┅┅┅┅┅┅┅14分
┅┅┅┅┅┅┅┅┅┅14分
练习册系列答案
相关题目
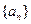 和
和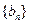 满足:
满足: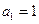 ,
,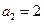 ,
,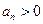 ,
,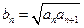 (
(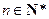 ),且
),且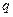 为公比的等比数列.
为公比的等比数列.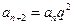 ;
;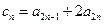 ,证明:数列
,证明:数列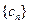 是等比数列;
是等比数列;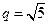 ,求和:
,求和: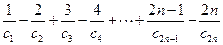 .
.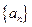 中,
中,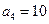 且
且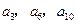 成等比数列,求数列
成等比数列,求数列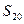 .
.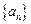 中,
中,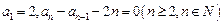 .
.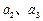 的值(只写结果)并求出数列
的值(只写结果)并求出数列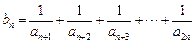 ,若对任意的正整数
,若对任意的正整数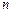 ,当
,当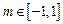 时,不等式
时,不等式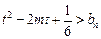 恒成立,求实数
恒成立,求实数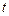 的取值范围。
的取值范围。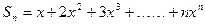
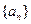 满足
满足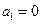 ,
,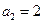 ,且对任意
,且对任意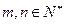 都有
都有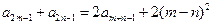
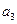 ,
,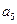 ;
;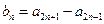
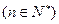 ,证明:
,证明: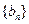 是等差数列;
是等差数列;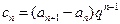
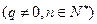 ,求数列
,求数列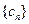 的前n项和
的前n项和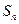 .
.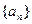 中,
中,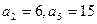 ,若
,若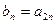 ,则数列
,则数列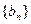 的前5项和等于( )
的前5项和等于( )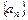 中,
中,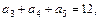 则
则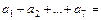 ( )
( )