函数f(x)=loga|x|在上单调递增.则f的大小关系是( )A．fB．fC．fD．不能确定题目和参考答案——青夏教育精英家教网—

题目内容

13．函数f（x）=log_a|x|在（-∞，0）上单调递增，则f（-3）与f（2）的大小关系是（　　）

A．

f（-3）=f（2）

B．

f（-3）＞f（2）

C．

f（-3）＜f（2）

D．

不能确定

分析先分析函数的奇偶性，进而结合函数f（x）=log_a|x|在（-∞，0）上单调递增，可得答案．

解答解：∵函数f（x）=log_a|x|满足f（-x）=f（x），
故f（2）=f（-2），
又∵函数f（x）=log_a|x|在（-∞，0）上单调递增，
∴f（-3）＜f（-2），
即f（-3）＜f（2），
故选：C

点评本题考查的知识点是函数单调性的性质，函数的奇偶性，是函数图象和性质的简单综合应用．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

4．计算：tan45°+cos60°÷lne=

$\frac{3}{2}$ ．

1．设函数f（x）=

$\left\{\begin{array}{l}{4x-4，x≤1}\\{{x}^{2}-4x+3，x＞1}\end{array}\right.$ ，g（x）=-

$\frac{1}{x}$ ，则函数h（x）=f（x）-g（x）的零点个数是（　　）

8．已知直线l过圆x²+y²-6y+5=0的圆心，且与直线x+y+5=0平行，则l的方程是（　　）

$\frac{{x}^{2}}{{a}^{2}}$ +

$\frac{{y}^{2}}{{b}^{2}}$ =1（a＞b＞0）的左、右焦点分别为F₁（-3，0）、F₂（3，0），直线y=kx与椭圆交于A、B两点．
（1）若三角形AF₁F₂的周长为

$4\sqrt{3}+6$ ，求椭圆的标准方程；
（2）若

$2\sqrt{3}＜a＜3\sqrt{2}$ ，且以AB为直径的圆过椭圆的右焦点，求直线y=kx斜率k的取值范围．

5．设集合A={x|x²-x=0}，B={x|log₂x≤0}，则A∪B=（　　）

2．

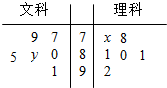某中学从文、理科实验班中各选6名同学去参加复旦大学自主招生考试，其数学成绩茎叶图如图，其中文科生的成绩的众数为85，理科生成绩平均数为81，则x•y的值为（　　）

$z=\frac{1-3i}{1+i}$ 的模是（　　）

$\sqrt{3}$

$\sqrt{5}$

试题分类