题目内容
1．设函数f（x）=$\left\{\begin{array}{l}{4x-4，x≤1}\\{{x}^{2}-4x+3，x＞1}\end{array}\right.$，g（x）=-$\frac{1}{x}$，则函数h（x）=f（x）-g（x）的零点个数是（ ）| A． | 4 | B． | 3 | C． | 2 | D． | 1 |
分析 作函数f（x）=$\left\{\begin{array}{l}{4x-4，x≤1}\\{{x}^{2}-4x+3，x＞1}\end{array}\right.$与函数g（x）=-$\frac{1}{x}$的图象，对0＜x≤1时单独讨论即可．
解答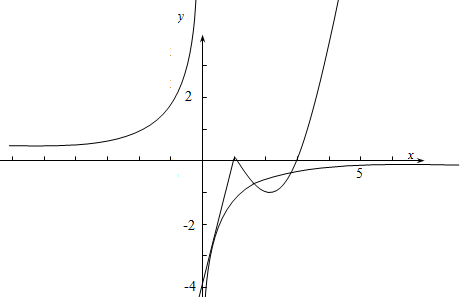 
解：作函数f（x）=$\left\{\begin{array}{l}{4x-4，x≤1}\\{{x}^{2}-4x+3，x＞1}\end{array}\right.$与函数g（x）=-$\frac{1}{x}$的图象如下，
，
当0＜x≤1时，h（x）=4x-4+$\frac{1}{x}$≥0，
（当且仅当4x=$\frac{1}{x}$，即x=$\frac{1}{2}$时，等号成立）；
故两个函数图象共有三个公共点，
故函数h（x）=f（x）-g（x）的零点个数是3，
故选：B．
点评 本题考查了数形结合的思想应用及基本不等式的应用．注意对0＜x≤1时单独讨论．
练习册系列答案
相关题目
11．设x，y满足约束条件：$\left\{\begin{array}{l}x-4y≤-3\\ 3x+5y≤25\\ x≥1\end{array}\right.$，则z=x+y的最大值是（ ）
| A． | $\frac{22}{5}$ | B． | 2 | C． | $\frac{27}{5}$ | D． | 7 |
6．某社团组织50名志愿者参加社会公益活动，帮助那些需要帮助的人，各位志愿者根据各自的实际情况，选择了两个不同的活动项目，相关的数据如下表所示：
（1）先用分层抽样的方法在做义工的志愿者中随机抽取6名志愿者，再从这6名志愿者中又随机抽取2名志愿者，设抽取的2名志愿者中女性人数为ξ，求ξ的数学期望．
（2）如果“宣传慰问”与“做义工”是两个分类变量，那么你有多大把握认为选择做宣传慰问与做义工是与性别有关系的？
附：2×2列联表随机变量K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$．P（K2≥k）与k对应值表：
| 宣传慰问 | 义工 | 总计 | |
| 男性志愿者 | 11 | 16 | 27 |
| 女性志愿者 | 15 | 8 | 23 |
| 总计 | 26 | 24 | 50 |
（2）如果“宣传慰问”与“做义工”是两个分类变量，那么你有多大把握认为选择做宣传慰问与做义工是与性别有关系的？
附：2×2列联表随机变量K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$．P（K2≥k）与k对应值表：
| 参考数据 | P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
13．函数f（x）=loga|x|在（-∞，0）上单调递增，则f（-3）与f（2）的大小关系是（ ）
| A． | f（-3）=f（2） | B． | f（-3）＞f（2） | C． | f（-3）＜f（2） | D． | 不能确定 |
10．若f（x）=x2+kx+1，an=f（n），n∈N*，已知数列{an}是递增数列，则k的取值范围是（ ）
| A． | [0，+∞） | B． | （-1，+∞） | C． | [-2，+∞） | D． | （-3，+∞） |
