题目内容
设 若
若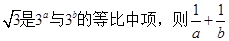 的最小值( )
的最小值( )
 若
若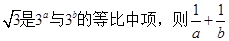 的最小值( )
的最小值( )A.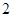 | B. | C. | D.8 |
C
试题分析:由题意可知,设
 若
若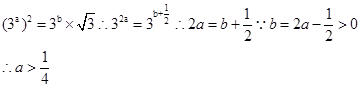
那么可知
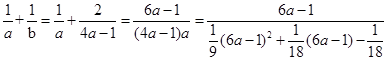
利用分子分母同时除以6a-1,然后结合均值不等式来求解得到最小值为4,故选C.
点评:解决该试题的关键是利用等比中项的性质,得到a,b的关系,然后借助于均值不等式来求解最值,考查了分析问题和解决问题的能力,属于中档题。

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
题目内容
 若
若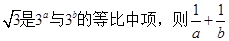 的最小值( )
的最小值( )A.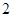 | B. | C. | D.8 |
 若
若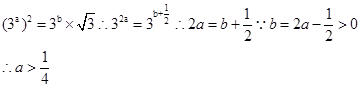
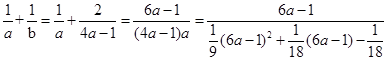

 中考解读考点精练系列答案
中考解读考点精练系列答案