题目内容
(本小题满分12分)
数列{an}的前n项和记为Sn,已知a1=1,an+1=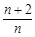 Sn(n=1,2,3…).
Sn(n=1,2,3…).
求证:数列{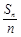 }是等比数列.
}是等比数列.
数列{an}的前n项和记为Sn,已知a1=1,an+1=
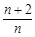 Sn(n=1,2,3…).
Sn(n=1,2,3…).求证:数列{
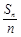 }是等比数列.
}是等比数列.{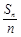 }是以2为公比的等比数列.
}是以2为公比的等比数列.
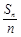 }是以2为公比的等比数列.
}是以2为公比的等比数列.试题分析:求证数列是否为等比数列,主要是看该数列的相邻两项的比值是否为定值,注意从第二项起来证明即可。证明:∵an+1=Sn+1-Sn,an+1=
 Sn, 3分
Sn, 3分∴(n+2)Sn=n(Sn+1-Sn),整理得nSn+1=2(n+1) Sn, 6分
所以
 =
= .又
.又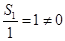 10分
10分故{
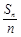 }是以2为公比的等比数列. 12分
}是以2为公比的等比数列. 12分点评:考查了等比数列的定义的运用,注意根据相邻项的比值为定值来得到结论,属于基础题。

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
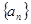 中,首项
中,首项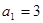 ,前三项和为21,则
,前三项和为21,则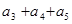 =( )
=( )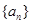 满足
满足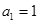 ,
,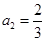 ,且
,且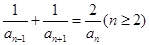 ,则
,则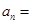
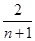

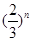
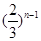
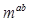 <1,则m的取值范围是( )
<1,则m的取值范围是( )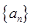 中,已知
中,已知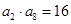 ,则
,则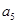 的值为( )
的值为( ) ,则
,则 _______________.
_______________.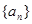 是公差不为零的等差数列,
是公差不为零的等差数列, 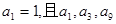 成等比数列.
成等比数列.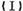 求数列
求数列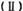 求数列
求数列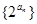 的前n项和
的前n项和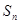
 若
若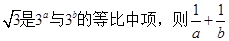 的最小值( )
的最小值( )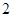


 中,各项都是正数,且3
中,各项都是正数,且3 ,
, 成等差数列,则
成等差数列,则