题目内容
在120°的二面角内，放一个半径为10cm的球切两半平面于A，B两点，那么这两切点在球面上的最短距离是______．
由球的性质知，OA，OB分别垂直于二面角的两个面，
又120°的二面角内，故∠AOB=60°
∵半径为10cm的球切两半平面于A，B两点
∴两切点在球面上的最短距离是10×
=
故答案为：
．
又120°的二面角内，故∠AOB=60°
∵半径为10cm的球切两半平面于A，B两点
∴两切点在球面上的最短距离是10×
| π |
| 3 |
| 10π |
| 3 |
故答案为：
| 10π |
| 3 |
练习册系列答案
相关题目
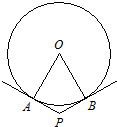（2008•普陀区一模）在120°的二面角内放一个半径为6的球，使球与两个半平面各只有一个公共点（其过球心且垂直于二面角的棱的直截面如图所示），则这两个公共点AB之间的球面距离为