题目内容
在120°的二面角内，放一个半径为10cm的球切两半平面于A，B两点，那么这两切点在球面上的最短距离是分析：由题意及二面角的面与球相切的性质可以求得∠AOB=60°，又半径已知，由弧长公式求出两切点在球面上的最短距离
解答：解：由球的性质知，OA，OB分别垂直于二面角的两个面，
又120°的二面角内，故∠AOB=60°
∵半径为10cm的球切两半平面于A，B两点
∴两切点在球面上的最短距离是10×
=
故答案为：
．
又120°的二面角内，故∠AOB=60°
∵半径为10cm的球切两半平面于A，B两点
∴两切点在球面上的最短距离是10×
| π |
| 3 |
| 10π |
| 3 |
故答案为：
| 10π |
| 3 |
点评：本题考查球面距离及相关计算，解题的关键是根据二面角与球的位置关系得出过两切点的两个半径的夹角以及球面上两点距离的公式，本题考查了空间想像能力，能根据题设条件想像出两个几何体的位置关系且判断出夹角是解题成功的保证
练习册系列答案
相关题目
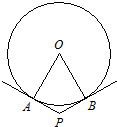（2008•普陀区一模）在120°的二面角内放一个半径为6的球，使球与两个半平面各只有一个公共点（其过球心且垂直于二面角的棱的直截面如图所示），则这两个公共点AB之间的球面距离为