题目内容
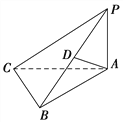
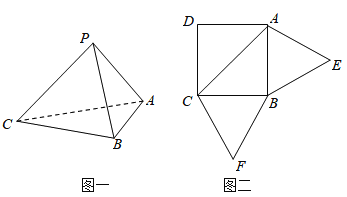
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() 、
、![]() ,
,![]() 为相圆
为相圆![]() 上一点,
上一点,![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过右焦点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 、
、![]() 两点若
两点若![]() 的中点为
的中点为![]() ,
,![]() 为原点,直线
为原点,直线![]() 交直线
交直线![]() 于点
于点![]() .求
.求![]() 的最大值.
的最大值.
【答案】(I)![]() ;(II)
;(II)![]()
【解析】
(Ⅰ)由题意得![]() ,通过平面几何的知识,可以得到
,通过平面几何的知识,可以得到![]() ,根据
,根据![]() ,离心率为
,离心率为![]() ,结合
,结合![]() ,这样可以求出
,这样可以求出![]() ,
,![]() ,进而求出椭圆的标准方程;
,进而求出椭圆的标准方程;
(II)直线与椭圆方程联立,可以得到一个一元二次方程,设![]() 、
、![]() ,利用根与系数关系可以求出
,利用根与系数关系可以求出![]() 的坐标,以及
的坐标,以及![]() 的长度,求出直线
的长度,求出直线![]() 的方程,求出
的方程,求出![]() 的坐标,求出
的坐标,求出![]() 的长度表达式,求出
的长度表达式,求出 ![]() 平方的表达式,用换元法、配方法,最后求出
平方的表达式,用换元法、配方法,最后求出![]() 的最大值.
的最大值.
(I)连接![]() ,由题意得
,由题意得![]() ,所以
,所以![]() 为
为![]() 的中位线,
的中位线,
又因为![]() ,所以
,所以![]() ,且
,且![]()
又![]() ,
,![]() ,得
,得![]() ,
,![]() ,
,
故所求椭圆方程为![]() .
.
(II)联立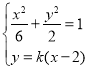 ,可得
,可得![]() .
.
设![]() 、
、![]() ,则
,则![]() ,
,![]() ,
,
所以为![]()
所以![]() 的中点
的中点![]() 坐标为
坐标为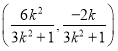 ,
,![]()
因此直线![]() 的方程为
的方程为![]() ,从而点
,从而点![]() 为
为![]() ,
,![]() ,
,
设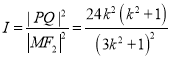 ,令
,令![]() ,则
,则
![]()
![]()
 ,
,
因此当![]() ,即
,即![]() 时
时![]() 取得最大值
取得最大值![]() .
.

【题目】党的十九大明确把精准脱贫作为决胜全面建成小康社会必须打好的三大攻坚战之一,为坚决打赢脱贫攻坚战,某帮扶单位为帮助定点扶贫村扶贫. 此帮扶单位为了了解某地区贫困户对其所提供的帮扶的满意度,随机调查了40个贫困户,得到贫困户的满意度评分如下:
贫困户编号 | 评分 | 贫困户编号 | 评分 | 贫困户编号 | 评分 | 贫困户编号 | 评分 | |||
1 2 3 4 5 6 7 8 9 10 | 78 73 81 92 95 85 79 84 63 86 | 11 12 13 14 15 16 17 18 19 20 | 88 86 95 76 97 78 88 82 76 89 | 21 22 23 24 25 26 27 28 29 30 | 79 83 72 74 91 66 80 83 74 82 | 31 32 33 34 35 36 37 38 39 40 | 93 78 75 81 84 77 81 76 85 89 |
用系统抽样法从40名贫困户中抽取容量为10的样本,且在第一分段里随机抽到的评分数据为92.
(1)请你列出抽到的10个样本的评分数据;
(2)计算所抽到的10个样本的均值![]() 和方差
和方差![]() ;
;
(3)在(2)条件下,若贫困户的满意度评分在![]() 之间,则满意度等级为“
之间,则满意度等级为“![]() 级”.运用样本估计总体的思想,现从(1)中抽到的10个样本的满意度为“
级”.运用样本估计总体的思想,现从(1)中抽到的10个样本的满意度为“![]() 级”贫困户中随机地抽取2户,求所抽到2户的满意度均评分均“超过80”的概率.
级”贫困户中随机地抽取2户,求所抽到2户的满意度均评分均“超过80”的概率.
(参考数据:![]() )
)
【题目】已知过原点的动直线![]() 与圆
与圆![]() :
:![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() .
.
(1)求圆![]() 的圆心坐标;
的圆心坐标;
(2)求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)是否存在实数![]() ,使得直线
,使得直线![]() :
:![]() 与曲线
与曲线![]() 只有一个交点?若存在,求出
只有一个交点?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
【题目】有一个同学家开了一个小卖部,他为了研究气温对热饮饮料销售的影响,经过统计,得到一个卖出的热饮杯数与当天气温的散点图和对比表:
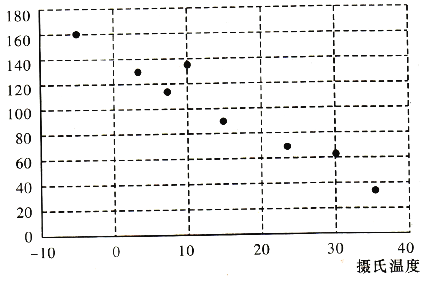
摄氏温度 |
|
|
|
|
|
|
|
|
热饮杯数 |
|
|
|
|
|
|
|
|
(1)从散点图可以发现,各点散布在从左上角到右下角的区域里。因此,气温与当天热饮销售杯数之间成负相关,即气温越高,当天卖出去的热饮杯数越少。统计中常用相关系数![]() 来衡量两个变量之间线性关系的强弱.统计学认为,对于变量
来衡量两个变量之间线性关系的强弱.统计学认为,对于变量![]() 、
、![]() ,如果
,如果![]() ,那么负相关很强;如果
,那么负相关很强;如果![]() ,那么正相关很强;如果
,那么正相关很强;如果![]() ,那么相关性一般;如果
,那么相关性一般;如果![]() ,那么相关性较弱。请根据已知数据,判断气温与当天热饮销售杯数相关性的强弱.
,那么相关性较弱。请根据已知数据,判断气温与当天热饮销售杯数相关性的强弱.
(2)(i)请根据已知数据求出气温与当天热饮销售杯数的线性回归方程;
(ii)记![]() 为不超过
为不超过![]() 的最大整数,如
的最大整数,如![]() ,
,![]() .对于(i)中求出的线性回归方程
.对于(i)中求出的线性回归方程![]() ,将
,将![]() 视为气温与当天热饮销售杯数的函数关系.已知气温
视为气温与当天热饮销售杯数的函数关系.已知气温![]() 与当天热饮每杯的销售利润
与当天热饮每杯的销售利润![]() 的关系是
的关系是![]()
![]() (单位:元),请问当气温
(单位:元),请问当气温![]() 为多少时,当天的热饮销售利润总额最大?
为多少时,当天的热饮销售利润总额最大?
(参考公式)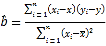 ,
,![]() ,
,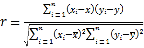
(参考数据)![]() ,
,![]() ,
,![]()
![]() .
.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
【题目】某社区消费者协会为了解本社区居民网购消费情况,随机抽取了100位居民作为样本,就最近一年来网购消费金额(单位:千元),网购次数和支付方式等进行了问卷调査.经统计这100位居民的网购消费金额均在区间![]() 内,按
内,按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6组,其频率分布直方图如图所示.
分成6组,其频率分布直方图如图所示.
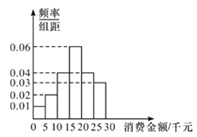
(1)估计该社区居民最近一年来网购消费金额的中位数;
(2)将网购消费金额在20千元以上者称为“网购迷”,补全下面的![]() 列联表,并判断有多大把握认为“网购迷与性别有关系”;
列联表,并判断有多大把握认为“网购迷与性别有关系”;
男 | 女 | 合计 | |
网购迷 | 20 | ||
非网购迷 | 45 | ||
合计 | 100 |
(3)调査显示,甲、乙两人每次网购采用的支付方式相互独立,两人网购时间与次数也互不. 影响.统计最近一年来两人网购的总次数与支付方式,所得数据如下表所示:
网购总次数 | 支付宝支付次数 | 银行卡支付次数 | 微信支付次数 | |
甲 | 80 | 40 | 16 | 24 |
乙 | 90 | 60 | 18 | 12 |
将频率视为概率,若甲、乙两人在下周内各自网购2次,记两人采用支付宝支付的次数之和为![]() ,求
,求![]() 的数学期望.
的数学期望.
附:观测值公式: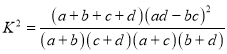
临界值表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |