题目内容
如图,在直三棱柱 中,
中, ,
, ,且异面直线
,且异面直线 与
与 所成的角等于
所成的角等于 .
.
(1)求棱柱的高;
(2)求 与平面
与平面 所成的角的大小.
所成的角的大小.
(1) ;(2)
;(2) .
.
解析试题分析:(1)由 得到
得到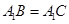 ,借助
,借助 异面直线
异面直线 与
与 所成的角等于
所成的角等于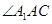 ,进而说明
,进而说明 为等边三角形,得出
为等边三角形,得出 的长度后再利用勾股定理求出
的长度后再利用勾股定理求出 的长,从而得到棱柱的高;(2)连接
的长,从而得到棱柱的高;(2)连接 交
交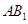 于点
于点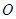 ,利用直线与平面垂直的判定定理证明
,利用直线与平面垂直的判定定理证明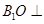 平面
平面 ,然后连接
,然后连接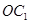 ,于是得到
,于是得到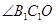 即为直线
即为直线 与平面
与平面 所成的角,最终在
所成的角,最终在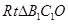 中计算相应的边长来求出
中计算相应的边长来求出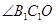 的大小.
的大小.
(1)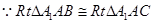 ,
,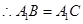
又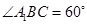 ,
,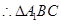 为正三角形,
为正三角形,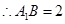 ,
,
所以棱柱的高为 ;
;
(2)连接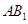 ,
,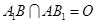 ,
,
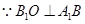 ,
, ,
, 平面
平面 ,
,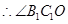 即为所求,
即为所求,
在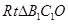 中,
中,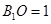 ,
, ,
,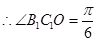 .
.
考点:1.异面直线所成的角;2.直线与平面所成的角

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 中,点
中,点 分别是棱
分别是棱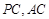 的中点.
的中点.  //平面
//平面 ;
; 平面
平面 ,
, ,求证:
,求证: .
.
 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱 ⊥底面
⊥底面  ,
, 是
是 的中点,作
的中点,作 交
交 于点
于点 .
.
 平面
平面 ;
; 的正弦值.
的正弦值. 
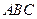 —
—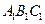 中,侧棱垂直底面,
中,侧棱垂直底面, ,
,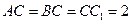 。
。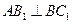 ;
; —
—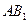 —
—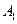 的大小。
的大小。 ,ED=1,
,ED=1, //BD,且
//BD,且 .
. 平面BDEF;
平面BDEF;

 平面ABCD,AD//BC,BC=2AD,
平面ABCD,AD//BC,BC=2AD, AC,Q是线段PB的中点.
AC,Q是线段PB的中点.
 平面PAC;
平面PAC; ,PA=
,PA= ,∠ABC=120°,G为线段PC上的点.
,∠ABC=120°,G为线段PC上的点. 的值.
的值.
 平面ABCD,E,F分别为MA,DC的中点,求证:
平面ABCD,E,F分别为MA,DC的中点,求证: