题目内容
如图,在三棱锥 中,点
中,点 分别是棱
分别是棱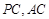 的中点.
的中点.
(1)求证: //平面
//平面 ;
;
(2)若平面 平面
平面 ,
, ,求证:
,求证: .
.
(1)详见解析;(2)详见解析.
解析试题分析:(1)题中条件出现了两个中点,故可考虑利用三角形中位线得到线线平行从而得到线面平行:即有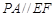 ,
,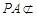 平面
平面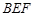 ,
,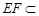 平面
平面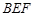 ,
, 平面
平面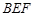 ;(2)由题中条件平面
;(2)由题中条件平面 平面
平面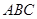 ,故可首先由面面垂直得到线面垂直,因此在平面
,故可首先由面面垂直得到线面垂直,因此在平面 内过点
内过点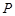 作
作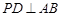 ,垂足为
,垂足为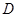 ,则有
,则有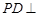 平面
平面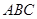 ,结合条件
,结合条件 ,可得
,可得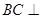 平面
平面 ,从而
,从而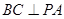 .
.
试题解析:(1)在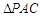 中,∵
中,∵ 、
、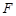 分别是
分别是 、
、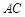 的中点,∴
的中点,∴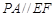 ,
,
又∵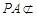 平面
平面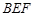 ,
,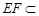 平面
平面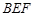 ,∴
,∴ 平面
平面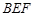 ; 6分
; 6分
(2)如图,在平面 内过点
内过点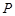 作
作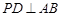 ,垂足为
,垂足为 .
.
∵平面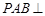 平面
平面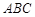 ,平面
,平面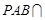 平面
平面 ,
, 平面
平面 ,
,
∴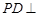 平面
平面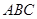 , 8分
, 8分
又∵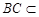 平面
平面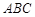 ,∴
,∴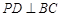 , 10分
, 10分
又∵ ,
,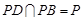 ,
, 平面
平面 ,
, 平面
平面 ,
,
∴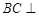 平面
平面 , 12分
, 12分
∵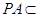 平面
平面 ,∴
,∴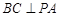 . 14分
. 14分
考点:1.线面平行的证明;2.线线垂直的证明.

练习册系列答案
相关题目

 平面
平面 ,且四边形
,且四边形 ,
, ,
, ,
, .
.
 平面
平面 ;(2)求平面
;(2)求平面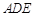 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
 中,底面
中,底面 是矩形,
是矩形,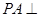 平面
平面 ,
, ,
, 依次是
依次是 的中点.
的中点.
 ;
; 与平面
与平面 所成角的正弦值.
所成角的正弦值. 中,已知平面
中,已知平面 平面
平面 且
且 ,
, .
.
 为棱
为棱 上的一点,且
上的一点,且 平面
平面 ,求线段
,求线段 的长度
的长度
 中,
中, 为矩形,平面
为矩形,平面 平面
平面

 问
问 为何值时,四棱锥
为何值时,四棱锥 与平面
与平面 夹角的余弦值.
夹角的余弦值. 和
和 都为矩形。
都为矩形。
 ,证明:直线
,证明:直线 平面
平面 ,
, 分别是线段
分别是线段 ,
, 的中点,在线段
的中点,在线段 上是否存在一点
上是否存在一点 ,使直线
,使直线 平面
平面 ?请证明你的结论。
?请证明你的结论。 和
和 所在平面互相垂直,且
所在平面互相垂直,且 ,
, ,E、F、G分别为AC、DC、AD的中点.
,E、F、G分别为AC、DC、AD的中点. 平面BCG;
平面BCG; ,其中S为底面面积,h为高.
,其中S为底面面积,h为高.
 中,
中, ,
, ,且异面直线
,且异面直线 与
与 所成的角等于
所成的角等于 .
.
 所成的角的大小.
所成的角的大小. 中,
中, ,它所在平面外一点
,它所在平面外一点 到
到 的距离是 .
的距离是 .