题目内容
某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60) ...[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题: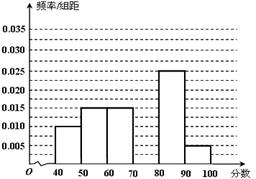
(Ⅰ)求成绩落在[70,80)上的频率,并补全这个频率分布直方图;
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)和平均分;
(Ⅲ) 从成绩是70分以上(包括70分)的学生中选两人,求他们在同一分数段的概率.
(Ⅰ)成绩落在[70,80)上的频率是0.3,频率分布直方图如下图. 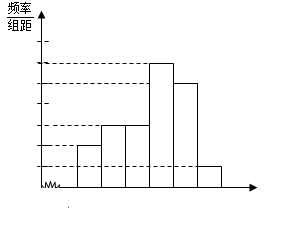
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)为75﹪,平均分71;
(Ⅲ)所求的概率为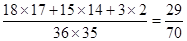 。
。
解析试题分析:(Ⅰ)成绩落在[70,80)上的频率是
0.3,频率分布直方图如下图.------4分
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)
为1-0.01×10-0.015×10=75﹪
平均分:45×0.1+55×0.15+65×0.15+75×0.3+85×0. 25+95×0.05=71-------8分
(Ⅲ) 成绩是70分以上(包括70分)的学
生人数为(0.03+0.025+0.005)×10×60=36
所以所求的概率为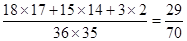 --12分
--12分
考点:本题主要考查频率、频数的概念及其关系,频率分布直方图及其应用。
点评:中档题,各小组频数之和等于数据总和,各小组频率之和等于1.频率、频数的关系:频率=频数÷数据总和。

(理科)PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,根据现行国家标准GB3095 – 2012,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米 ~ 75毫克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标。从某自然保护区2012年全年每天的PM2.5监测值数据中随机地抽取10天的数据作为样本,监测值频数如下表所示:
| PM2.5日均值 (微克/立方米) | [25,35] | (35,45] | (45,55] | (55,65] | (65,75] | (75,85] |
| 频数 | 3 | 1 | 1 | 1 | 1 | 3 |
某车间为了规定工时额,需确定加工零件所花费的时间,为此做了4次试验,得到的数据如下图:若加工时间 与零件个数
与零件个数 之间有较好的线性相关关系。(
之间有较好的线性相关关系。(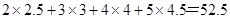 )
)
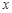 | 2 | 3 | 4 | 5 |
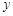 | 2.5 | 3 | 4 | 4.5 |
(1)求加工时间与零件个数的线性回归方程;
(2)试预报加工10个零件需要的时间。
(附:回归方程系数公式
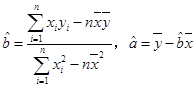 )
) 某市居民1999~2003年货币收入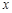 与购买商品支出
与购买商品支出 的统计资料如下表所示:单位:亿元
的统计资料如下表所示:单位:亿元
| 年份 | 1999 | 2000 | 2001 | 2002 | 2003 |
货币收入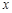 | 40 | 42 | 44 | 47 | 50 |
购买商品支出 | 33 | 34 | 36 | 39 | 41 |

(Ⅱ)已知
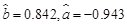 ,请写出Y对x的回归直 线方程,并估计货币收入为52(亿元)时,购买商品支出大致为多少亿元?
,请写出Y对x的回归直 线方程,并估计货币收入为52(亿元)时,购买商品支出大致为多少亿元? (本题10分) 为了解高二学年女生身高情况,对高二(10)班女生身高进行了一次测量,所得数据整理后列出了频率分布表如下:
| 组 别 | 频数 | 频率 |
| 145.5~149.5 | 1 | 0.02 |
| 149.5~153.5 | 4 | 0.08 |
| 153.5~157.5 | 20 | 0.40 |
| 157.5~161.5 | 15 | 0.30 |
| 161.5~165.5 | 8 | 0.16 |
| 165.5~169.5 | m | n |
| 合 计 | M | N |
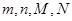 所表示的数分别是多少?
所表示的数分别是多少?(2)若该校高二学年共有女生500人,试估计高二女生中身高在161.5以上的人数。
(本小题满分12分)某公司欲招聘员工,从1000名报名者中筛选200名参加笔试,按笔试成绩择优取50名面试,再从面试对象中聘用20名员工.
(1)求每个报名者能被聘用的概率;
(2)随机调查了24名笔试者的成绩如下表所示:
| 分数段 | [60,65) | [65,70) | [70,75) | [75,80) | [80,85) | [85,90) |
| 人数 | 1 | 2 | 6 | 9 | 5 | 1 |
(3)公司从聘用的四男
 、
、 、
、 、
、 和二女
和二女 、
、 中选派两人参加某项培训,则选派结果为一男一女的概率是多少?
中选派两人参加某项培训,则选派结果为一男一女的概率是多少? (本小题满分10分)国家有甲,乙两个射击队,若两个队共进行了8次热身赛,
各队的总成绩见下表:
| 甲队 | 403 | 390 | 397 | 404 | 388 | 400 | 412 | 406 |
| 乙队 | 417 | 401 | 410 | 416 | 406 | 421 | 398 | 411 |
分别求两个队总成绩的样本平均数和样本方差,根据计算结果,若选一个代表队参加奥运会比赛,你认为应该选哪一个队?
 的列联表;(2)能否在犯错误的概率不超过0.05的前提下认为晕机与性别有关?
的列联表;(2)能否在犯错误的概率不超过0.05的前提下认为晕机与性别有关?