题目内容
某车间为了规定工时额,需确定加工零件所花费的时间,为此做了4次试验,得到的数据如下图:若加工时间 与零件个数
与零件个数 之间有较好的线性相关关系。(
之间有较好的线性相关关系。(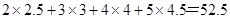 )
)
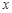 | 2 | 3 | 4 | 5 |
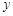 | 2.5 | 3 | 4 | 4.5 |
(1)求加工时间与零件个数的线性回归方程;
(2)试预报加工10个零件需要的时间。
(附:回归方程系数公式
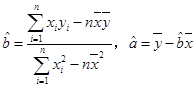 )
)
(1)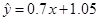 (2)约需要8.05小时
(2)约需要8.05小时
解析试题分析:(1)根据表中数据可以求出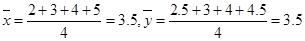 ,
,
根据公式可以求出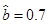 ,
,
再代入公式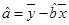 ,可以求得
,可以求得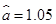
所以回归直线方程为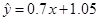 ; 10分
; 10分
(2)将x=10代入求出的回归直线中,可以解得
所以加工10个零件约需要8.05小时。 13分
考点:本小题主要考查回归直线方程的求解和应用.
点评:当变量之间具有线性相关关系时,求出的回归直线才有意义,另外,由回归直线得到的是估计值,而不是精确值.

练习册系列答案
相关题目
(文科)(本小题满分12分)某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本,得频率分布表如下:
| 组号 | 分组 | 频数 | 频率 |
| 第一组 | [230,235) | 8 | 0.16 |
| 第二组 | [235,240) | ① | 0.24 |
| 第三组 | [240,245) | 15 | ② |
| 第四组 | [245,250) | 10 | 0.20 |
| 第五组 | [250,255] | 5 | 0.10 |
| 合 计 | 50 | 1.00 | |
(2)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,分别求第三、四、五各组参加考核人数;
(3)在(2)的前提下,高校决定在这6名学生中录取2名学生,求2人中至少有1名是第四组的概率.
某设备的使用年限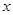 与所支出的总费用
与所支出的总费用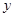 (万元)有如下的统计资料:
(万元)有如下的统计资料:
使用年限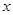 | 1 | 2 | 3 | 4 |
总费用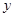 | 1.5 | 2 | 3 | 3.5 |

(Ⅱ)求出
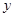 关于
关于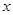 的线性回归方程
的线性回归方程 ;
;(III)当使用10年时,所支出的总费用约为多少万元。
参考公式:回归方程为
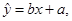 其中
其中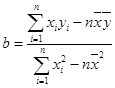 ,
, 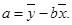
以下是某地搜集到的新房屋的销售价格 和房屋的面积
和房屋的面积 的数据:
的数据:
房屋面积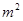 | 110 | 90 | 80 | 100 | 120 |
| 销售价格(万元) | 33 | 31 | 28 | 34 | 39 |
(2)求线性回归方程;
(3)据(2)的结果估计当房屋面积为
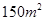 时的销售价格.
时的销售价格.(提示:
 ,
, 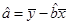 ,
,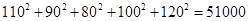 ,
,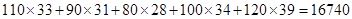 )
) (本小题满分12分)为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有800名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计. 请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
| 分组 | 频数 | 频率 |
| 50.5~60.5 | 6 | 0.08 |
| 60.5~70.5 | | 0.16 |
| 70.5~80.5 | 15 | |
| 80.5~90.5 | 24 | 0.32 |
| 90.5~100.5 | | |
| 合计 | 75 | |
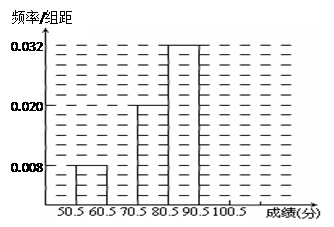
(Ⅰ)填充频率分布表的空格(将答案直接填在答题卡的表格内);
(Ⅱ)补全频率分布直方图;
(Ⅲ)若成绩在75.5~85.5分的学生为二等奖,问获得二等奖的学生约为多少人?
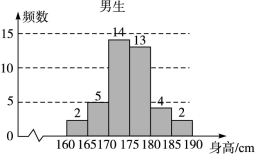
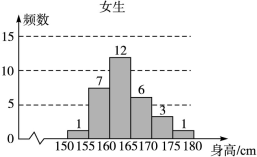

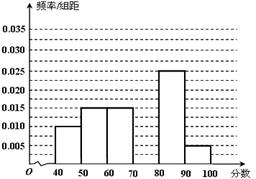

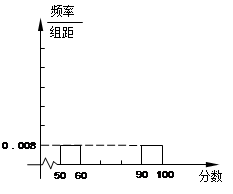
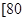 ,
,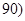 之间的矩形的高,并完成直方图;
之间的矩形的高,并完成直方图;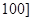 之间任取两份进行分析,在抽取的结果中,求至少有一份分数在
之间任取两份进行分析,在抽取的结果中,求至少有一份分数在 ,
,