题目内容
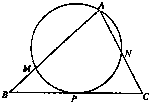 如图,已知△ABC,过顶点A的圆与边BC切于BC的中点P,与边AB、AC分别交于点M、N,且CN=2BM,点N平分AC.则
如图,已知△ABC,过顶点A的圆与边BC切于BC的中点P,与边AB、AC分别交于点M、N,且CN=2BM,点N平分AC.则| AM |
| BM |
分析:由切割线定理,得BP2=BM•BA,CP2=CN•CA,由BP=CP,知BM•BA=2CN2,由CN=NA=2BM,BA=BM+AM,能够证明AM=7BM.
解答:证明:由切割线定理,得BP2=BM•BA,CP2=CN•CA,…(5分)
∵BP=CP,∴BM•BA=2CN2,
∵CN=NA=2BM,BA=BM+AM,
∴BM(BM+AM)=8BM2,
∴AM=7BM,…(10分)
则
=7.
故选D.
∵BP=CP,∴BM•BA=2CN2,
∵CN=NA=2BM,BA=BM+AM,
∴BM(BM+AM)=8BM2,
∴AM=7BM,…(10分)
则
| AM |
| BM |
故选D.
点评:本题考查与圆有关的比例线段的求法,解题时要认真审题,注意切割线定理的合理运用.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
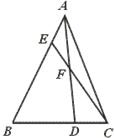 如图,已知△ABC中,AE:EB=1:3,BD:DC=2:1,AD与CE相交于F.求
如图,已知△ABC中,AE:EB=1:3,BD:DC=2:1,AD与CE相交于F.求 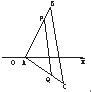 如图,已知△ABC的顶点坐标依次为A(1,0),B(5,8),C(7,-4),在边AB上有一点P,其横坐标为4,在AC上求一点Q,使线段PQ把△ABC分成面积相等的两部分.
如图,已知△ABC的顶点坐标依次为A(1,0),B(5,8),C(7,-4),在边AB上有一点P,其横坐标为4,在AC上求一点Q,使线段PQ把△ABC分成面积相等的两部分.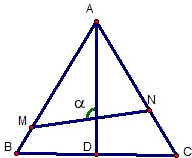 如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点,线段MN经过△ABC的中心G,设?MGA=a(
如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的点,线段MN经过△ABC的中心G,设?MGA=a( 如图,已知△ABC的外角∠EAC的平分线与△ABC的外接圆交于点D,以CD为直径的圆分别交BC,CA于点P、Q,求证:线段PQ平分△ABC的周长.
如图,已知△ABC的外角∠EAC的平分线与△ABC的外接圆交于点D,以CD为直径的圆分别交BC,CA于点P、Q,求证:线段PQ平分△ABC的周长.