题目内容
 如图,已知△ABC的外角∠EAC的平分线与△ABC的外接圆交于点D,以CD为直径的圆分别交BC,CA于点P、Q,求证:线段PQ平分△ABC的周长.
如图,已知△ABC的外角∠EAC的平分线与△ABC的外接圆交于点D,以CD为直径的圆分别交BC,CA于点P、Q,求证:线段PQ平分△ABC的周长.分析:如图,连接DB,DP,DQ,PQ.利用四边形外接圆的性质、角平分线的性质可得∠DBC=∠DCB,故△DBC为等腰三角形.于是DP⊥BC,则CP=
BC.在圆内接四边形ABCD中,由托勒密定理得:AC•BD=BC•AD+AB•CD,及BD=CD,可得AC-AB=
=
,又DQ⊥AC,可得△ADQ∽△BDP,可得
=
,即AQ=
.故AC-AB=2AQ,即AQ=
.可得CQ+CP=(AC-AQ)+
BC,把AQ代入即可.
| 1 |
| 2 |
| BC•AD |
| BD |
| 2BP•AD |
| BD |
| AQ |
| BP |
| AD |
| BD |
| BP•AD |
| BD |
| AC-AB |
| 2 |
| 1 |
| 2 |
解答:证:如图,连接DB,DP,DQ,PQ.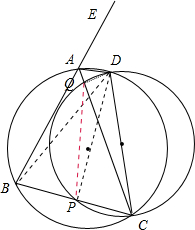
∵∠ABD=∠ACD,∠EAC=∠ABC+∠ACB,
∴∠EAC=∠DBC+∠DCB,即:2∠DAC=∠DBC+∠DCB;
又∠DAC=∠DBC,∴∠DBC=∠DCB,故△DBC为等腰三角形.
∵DP⊥BC,则CP=
BC.
在圆内接四边形ABCD中,由托勒密定理得:AC•BD=BC•AD+AB•CD,
∵BD=CD,∴AC-AB=
=
,
又DQ⊥AC,∴△ADQ∽△BDP,
∴
=
,即AQ=
.
故AC-AB=2AQ,即AQ=
.
∴CQ+CP=(AC-AQ)+
BC=(AC-
)+
BC=
(AB+BC+CA).

∵∠ABD=∠ACD,∠EAC=∠ABC+∠ACB,
∴∠EAC=∠DBC+∠DCB,即:2∠DAC=∠DBC+∠DCB;
又∠DAC=∠DBC,∴∠DBC=∠DCB,故△DBC为等腰三角形.
∵DP⊥BC,则CP=
| 1 |
| 2 |
在圆内接四边形ABCD中,由托勒密定理得:AC•BD=BC•AD+AB•CD,
∵BD=CD,∴AC-AB=
| BC•AD |
| BD |
| 2BP•AD |
| BD |
又DQ⊥AC,∴△ADQ∽△BDP,
∴
| AQ |
| BP |
| AD |
| BD |
| BP•AD |
| BD |
故AC-AB=2AQ,即AQ=
| AC-AB |
| 2 |
∴CQ+CP=(AC-AQ)+
| 1 |
| 2 |
| AC-AB |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了四边形外接圆的性质、角平分线的性质、等腰三角形的性质、托勒密定理、相似三角形的性质等基础知识与基本方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
 如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使
如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使 如图,已知△ABC的顶点坐标依次为A(1,0),B(5,8),C(7,-4),在边AB上有一点P,其横坐标为4,在AC上求一点Q,使线段PQ把△ABC分成面积相等的两部分.
如图,已知△ABC的顶点坐标依次为A(1,0),B(5,8),C(7,-4),在边AB上有一点P,其横坐标为4,在AC上求一点Q,使线段PQ把△ABC分成面积相等的两部分. 如图,已知△ABC的顶点为A(2,4),B(0,-2),C(-2,3),求:
如图,已知△ABC的顶点为A(2,4),B(0,-2),C(-2,3),求: 是边长为2的正三角形,则原△ABC的面积为__________.
是边长为2的正三角形,则原△ABC的面积为__________.