题目内容
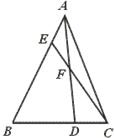如图，已知△ABC中，AE：EB=1：3，BD：DC=2：1，AD与CE相交于F．求 | EF |
| FC |
| AF |
| FD |
分析：先过E作EG∥BC，交AD于G，再作DH∥BC交CE于H，由平行线分线段成比例定理的推论，再结合已知条件，可分别求出
和
的值，相加即可．
| EF |
| EC |
| AF |
| AD |
解答：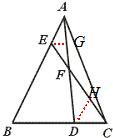
解：作EG∥BC交AD于G，则有
=
，即
=
，得
EG=
BD=
CD，
∴
=
=
作DH∥AB交CE于H，则DH=
BE=AE，
∴
=
=1，
∴
+
=
+1=
．
解：作EG∥BC交AD于G，则有 | AE |
| EB |
| 1 |
| 3 |
| AE |
| AB |
| 1 |
| 4 |
EG=
| 1 |
| 4 |
| 1 |
| 2 |
∴
| EF |
| FC |
| EG |
| CD |
| 1 |
| 2 |
作DH∥AB交CE于H，则DH=
| 1 |
| 3 |
∴
| AF |
| FD |
| AE |
| DH |
∴
| EF |
| FC |
| AF |
| FD |
| 1 |
| 2 |
| 3 |
| 2 |
点评：此题考查了相似三角形的性质：相似三角形的对应角相等，对应边的比相等，解题时要注意比例式的变形．
练习册系列答案
相关题目
如图，已知△ABC中的两条角平分线AD和CE相交于H，∠B=60°，F在AC上，
如图，已知△ABC中，
（2012•石家庄一模）如图，已知△ABC中，AB=