题目内容
【题目】某公司研究开发了一种新产品,生产这种新产品的年固定成本为150万元,每生产![]() 千件,需另投入成本为
千件,需另投入成本为![]() (万元),
(万元), 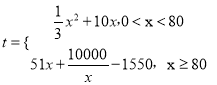 .每件产品售价为500元.该新产品在市场上供不应求可全部卖完.
.每件产品售价为500元.该新产品在市场上供不应求可全部卖完.
(Ⅰ)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(Ⅱ)当年产量为多少千件时,该公司在这一新产品的生产中所获利润最大?
【答案】(Ⅰ)  ;(Ⅱ) 100千件.
;(Ⅱ) 100千件.
【解析】试题分析:
(1)利用题意将利润函数写成分段函数的形式即可;
(2)结合(1)中函数的定义域和解析式可得当年产量为100千件时,该公司在这一新产品的生产中所获利润最大.
试题解析:
(Ⅰ)因为每件商品售价为500元,则![]() 千件商品销售额为50
千件商品销售额为50![]() 万元,依题意得
万元,依题意得
当![]() 时,
时, ![]() =
=![]()
当![]() 时,
时, ![]()
=![]() .
.
所以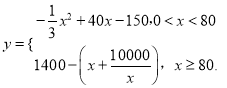
(Ⅱ)当![]() 时,
时, ![]()
此时,当![]() 千件时,
千件时, ![]() 取得最大值1050万元.
取得最大值1050万元.
当![]() 时,
时,

此时,当![]() 时,即
时,即![]() 千件时
千件时![]() 取得最大值1200万元.
取得最大值1200万元.
因为![]() ,
,
所以当产量为100千件时,该公司在这一新产品生产中所获利润最大,最大利润为1200万元.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某商场经销某商品,根据以往资料统计,顾客采用的付款期数![]() 的分布列为:
的分布列为:
| 1 | 2 | 3 | 4 | 5 |
| 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
商场经销该商品,可采用不同形式的分期付款,付款的期数![]() (单位:
(单位: ![]() )与商场经销一件商品的利润
)与商场经销一件商品的利润![]() (单位:元)满足如下关系:
(单位:元)满足如下关系: 
(Ⅰ)若记事件“购买该商品的3位顾客中,至少有1位采用一次性全额付款方式”为![]() ,试求事件
,试求事件![]() 的概率
的概率![]() ;
;
(Ⅱ)求商场经销一件商品的利润![]() 的分布列及期望
的分布列及期望![]() .
.