题目内容
【题目】某校高二理科8班共有50名学生参加学业水平模拟考试,成绩(单位:分,满分100分)大于或等于90分的为优秀,其中语文成绩近似服从正态分布![]() ,数学成绩的频率分布直方图如图.
,数学成绩的频率分布直方图如图.
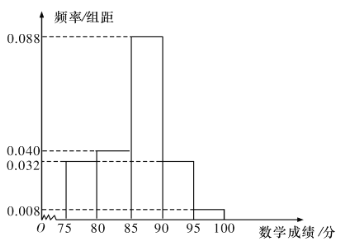
(I)这50名学生中本次考试语文、数学成绩优秀的大约各有多少人?
(Ⅱ)如果语文和数学两科成绩都优秀的共有4人,从语文优秀或数学优秀的这些同学中随机抽取3人,设3人中两科都优秀的有![]() 人,求
人,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)根据(I)(Ⅱ)的数据,是否有99%以上的把握认为语文成绩优秀的同学,数学成绩也优秀?
附:①若![]() ~
~![]() ,则
,则![]() ,
,![]() ;
;
②![]() ;
;
③
【答案】(Ⅰ) 语文成绩优秀的同学有8人,数学成绩优秀的同学有10人. (Ⅱ)见解析.( Ⅲ) 没有99%以上的把握认为语文成绩优秀的同学,数学成绩也优秀.
【解析】
(I)语文成绩服从正态分布,根据正态分布的![]() 原则可得语文成绩优秀的概率及人数;根据数学成绩的频率分布直方图可以计算数学成绩优秀的概率及人数;(Ⅱ)语文和数学两科成绩都优秀的共有4人,则语文单科优秀的4人,数学单科优秀的6人,即单科优秀的共10人,随机抽取3人,3人中两科都优秀的可能为0、1、2、3四种情况,服从超几何分布,利用概率公式分别求出每种情况的概率,即可写出X的分布列及数学期望;(Ⅲ)先填写列联表,利用公式求出
原则可得语文成绩优秀的概率及人数;根据数学成绩的频率分布直方图可以计算数学成绩优秀的概率及人数;(Ⅱ)语文和数学两科成绩都优秀的共有4人,则语文单科优秀的4人,数学单科优秀的6人,即单科优秀的共10人,随机抽取3人,3人中两科都优秀的可能为0、1、2、3四种情况,服从超几何分布,利用概率公式分别求出每种情况的概率,即可写出X的分布列及数学期望;(Ⅲ)先填写列联表,利用公式求出![]() 的值比较它与6.635的大小即可。
的值比较它与6.635的大小即可。
(Ⅰ)∵语文成绩服从正态分布![]() ,
,
∴语文成绩优秀的概率为![]() ,
,
数学成绩优秀的概率为![]() ,
,
∴语文成绩优秀的同学有![]() 人,
人,
数学成绩优秀的同学有![]() 人.
人.
(Ⅱ)语文数学两科都优秀的有4人,单科优秀的有10人,
![]() 的所有可能取值为0,1,2,3,
的所有可能取值为0,1,2,3,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
∴![]() 的分布列为:
的分布列为:
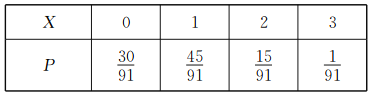
![]() .
.
(Ⅲ)![]() 列联表:
列联表:
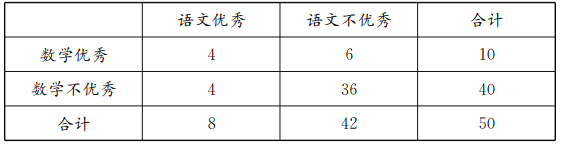
∴![]() .
.
∴没有99%以上的把握认为语文成绩优秀的同学,数学成绩也优秀.

【题目】一个工厂在某年连续10个月每月产品的总成本y(万元)与该月产量x(万件)之间有如下一组数据:
x | 1.08 | 1.12 | 1.19 | 1.28 | 1.36 | 1.48 | 1.59 | 1.68 | 1.80 | 1.87 |
y | 2.25 | 2.37 | 2.40 | 2.55 | 2.64 | 2.75 | 2.92 | 3.03 | 3.14 | 3.26 |
(1)通过画散点图,发现可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)①建立月总成本y与月产量x之间的回归方程;
②通过建立的y关于x的回归方程,估计某月产量为1.98万件时,此时产品的总成本为多少万元?
(均精确到0.001)
附注:①参考数据:![]() ,
,
![]() ,
,
②参考公式:相关系数 ,
,
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: .
.
【题目】武汉市摄影协会准备在2020年1月举办主题为“我们都是追梦人”摄影图片展,通过平常人的镜头记录国强民富的幸福生活,摄影协会收到了来自社会各界的大量作品,打算从众多照片中选取100张照片展出,其参赛者年龄集中![]() 在之间,根据统计结果,做出频率分布直方图如图:
在之间,根据统计结果,做出频率分布直方图如图:

(1)求频率直方图中![]() 的值,并根据频率直方图,求这100位摄影者年龄的中位数;
的值,并根据频率直方图,求这100位摄影者年龄的中位数;
(2)为了展示不同年龄作者眼中的幸福生活,摄影协会按照分层抽样的方法,计划从这100件照片中抽出20个最佳作品,并邀请相应作者参加“讲述照片背后的故事”座谈会.
①在答题卡上的统计表中填出每组相应抽取的人数:
年龄 |
|
|
|
|
|
人数 |
②若从年龄在![]() 的作者中选出2人把这些图片和故事整理成册,求这2人中至少有1人的年龄在
的作者中选出2人把这些图片和故事整理成册,求这2人中至少有1人的年龄在![]() 的概率.
的概率.