题目内容

选修4-4：坐标系与参数方程
已知极坐标系的极点是直角坐标系的原点，极轴与直角坐标系中x轴的正半轴重合．曲线C的极坐标方程为ρ=2cosθ-2sinθ，曲线l的极坐标方程是ρ（cosθ-2sinθ）=2．
（Ⅰ）求曲线C和l的直角坐标方程并画出草图；
（Ⅱ）设曲线C和l相交于A，B两点，求|AB|．
分析：（Ⅰ）利用ρcosθ=x，ρsinθ=y，把曲线的极坐标方程转化为直角坐标方程，然后画出草图；
（Ⅱ）直接利用圆心到直线的距离、半径、半弦长满足勾股定理，求出|AB|．
解答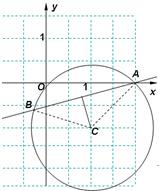：解：（Ⅰ）由ρcosθ=x，ρsinθ=y，得
曲线C的极坐标方程为ρ=2cosθ-2sinθ，即ρ2=2ρcosθ-2ρsinθ，
可化为直角坐标方程：x2+y2=2x-2y，（x-1）2+（y+1）2=2；
曲线l的极坐标方程是ρ（cosθ-2sinθ）=2．
可化为l的直角坐标方程：x-2y-2=0．------（5分）
（Ⅱ）设圆C的圆心C（1，-1）到直线l的距离为d，
则d=
|1-2(-1)-2|
5
=
5
5
，
所以|AB|=2
(
2
)2-(
5
5
)2
=
6
5
5
．----（10分）
点评：本题是中档题，考查曲线的极坐标方程与直角坐标方程的互化，点到直线的距离公式的应用，考查计算能力转化思想．
练习册系列答案
相关题目
[选修4-4：坐标系与参数方程]
在直角坐标系xoy中，直线l的参数方程为
x=
1
2
t
y=
2
2
+
3
2
t
（t为参数），若以直角坐标系xoy 的O点为极点，Ox为极轴，且长度单位相同，建立极坐标系，得曲线C的极坐标方程为ρ=2cos（θ-
π
4
）．直线l与曲线C交于A，B两点，求|AB|．
A．选修4-1：几何证明选讲
如图，△ABC的外接圆的切线AE与BC的延长线相交于点E，∠BAC的平分线与BC
交于点D．求证：ED2=EB•EC．
B．选修4-2：矩阵与变换
求矩阵M=
-14
26
的特征值和特征向量．
C．选修4-4：坐标系与参数方程
在以O为极点的极坐标系中，直线l与曲线C的极坐标方程分别是ρcos(θ+
π
4
)=
3
2
2
和ρsin2θ=4cosθ，直线l与曲线C交于点．A，B，C，求线段AB的长．
D．选修4-5：不等式选讲
对于实数x，y，若|x-1|≤1，|y-2|≤1，求|x-y+1|的最大值．
（2013•辽宁）选修4-4：坐标系与参数方程
在直角坐标系xoy中以O为极点，x轴正半轴为极轴建立坐标系．圆C1，直线C2的极坐标方程分别为ρ=4sinθ，ρcos（θ-
π
4
）=2
2
．
（Ⅰ）求C1与C2交点的极坐标；
（Ⅱ）设P为C1的圆心，Q为C1与C2交点连线的中点，已知直线PQ的参数方程为
x=t3+a
y=
b
2
t3+1
（t∈R为参数），求a，b的值．
选修4-4：
坐标系与参数方程在平面直角坐标系x0y中，曲线C1为x=acosφ，y=sinφ（1＜a＜6，φ为参数）．
在以0为原点，x轴正半轴为极轴的极坐标中，曲线C2的方程为ρ=6cosθ，射线ι为θ=α，ι与C1的交点为A，ι与C2除极点外的一个交点为B．当α=0时，|AB|=4．
（1）求C1，C2的直角坐标方程；
（2）若过点P（1，0）且斜率为
3
的直线m与曲线C1交于D、E两点，求|PD|与|PE|差的绝对值．
（2011•晋中三模）选修4-4：坐标系与参数方程选讲
在直角坐标系xoy中，曲线c1的参数方程为：
x=2cosθ
y=2sinθ
（θ为参数），把曲线c1上所有点的纵坐标压缩为原来的一半得到曲线c2，以O为极点，x正半轴为极轴建立极坐标系，直线l的极坐标方程为
2
ρcos(θ-
π
4
)=4．
（1）求曲线c2的普通方程，并指明曲线类型；
（2）过（1，0）点与l垂直的直线l1与曲线c2相交与A、B两点，求弦AB的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网