题目内容
(2013•辽宁)选修4-4:坐标系与参数方程
在直角坐标系xoy中以O为极点,x轴正半轴为极轴建立坐标系.圆C1,直线C2的极坐标方程分别为ρ=4sinθ,ρcos(θ-
)=2
.
(Ⅰ)求C1与C2交点的极坐标;
(Ⅱ)设P为C1的圆心,Q为C1与C2交点连线的中点,已知直线PQ的参数方程为
(t∈R为参数),求a,b的值.
在直角坐标系xoy中以O为极点,x轴正半轴为极轴建立坐标系.圆C1,直线C2的极坐标方程分别为ρ=4sinθ,ρcos(θ-
| π |
| 4 |
| 2 |
(Ⅰ)求C1与C2交点的极坐标;
(Ⅱ)设P为C1的圆心,Q为C1与C2交点连线的中点,已知直线PQ的参数方程为
|
分析:(I)先将圆C1,直线C2化成直角坐标方程,再联立方程组解出它们交点的直角坐标,最后化成极坐标即可;
(II)由(I)得,P与Q点的坐标分别为(0,2),(1,3),从而直线PQ的直角坐标方程为x-y+2=0,由参数方程可得y=
x-
+1,从而构造关于a,b的方程组,解得a,b的值.
(II)由(I)得,P与Q点的坐标分别为(0,2),(1,3),从而直线PQ的直角坐标方程为x-y+2=0,由参数方程可得y=
| b |
| 2 |
| ab |
| 2 |
解答:解:(I)圆C1,直线C2的直角坐标方程分别为 x2+(y-2)2=4,x+y-4=0,
解
得
或
,
∴C1与C2交点的极坐标为(4,
).(2
,
).
(II)由(I)得,P与Q点的坐标分别为(0,2),(1,3),
故直线PQ的直角坐标方程为x-y+2=0,
由参数方程可得y=
x-
+1,
∴
,
解得a=-1,b=2.
解
|
|
|
∴C1与C2交点的极坐标为(4,
| π |
| 2 |
| 2 |
| π |
| 4 |
(II)由(I)得,P与Q点的坐标分别为(0,2),(1,3),
故直线PQ的直角坐标方程为x-y+2=0,
由参数方程可得y=
| b |
| 2 |
| ab |
| 2 |
∴
|
解得a=-1,b=2.
点评:本题主要考查把极坐标方程化为直角坐标方程、把参数方程化为普通方程的方法,方程思想的应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•辽宁)(选修4-1几何证明选讲)
(2013•辽宁)(选修4-1几何证明选讲)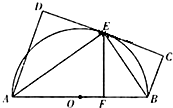 (2013•辽宁)选修4-1:几何证明选讲
(2013•辽宁)选修4-1:几何证明选讲