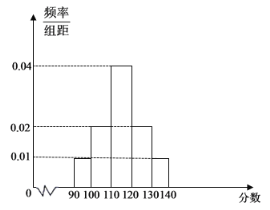
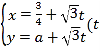题目内容
【题目】设函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)当![]() 时,记
时,记![]() 的最小值为
的最小值为![]() ,证明:
,证明:![]() .
.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.(2)见解析.
上单调递增.(2)见解析.
【解析】
(1)由题意可得![]() 的定义域为
的定义域为![]() ,求出
,求出![]() 的导函数,通过判断导函数的符号即可判断
的导函数,通过判断导函数的符号即可判断![]() 的单调性;
的单调性;
(2)由(1)可得![]() ,要证
,要证![]() ,即证
,即证![]() ,即证明
,即证明![]() ,通过构造函数
,通过构造函数![]() ,判断函数
,判断函数![]() 的单调性,通过求得函数
的单调性,通过求得函数![]() 的最大值即可推出结果.
的最大值即可推出结果.
(1)根据题意,可得![]() 的定义域为
的定义域为![]() ,
,
对![]() 求导可得:
求导可得:![]() ,
,
因为![]() ,当
,当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,令
时,令![]() 可得
可得![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() ,此时
,此时![]() 在
在![]() 单调递减,
单调递减,
当![]() 时,
时,![]() ,即
,即![]() ,此时
,此时![]() 在
在![]() 单调递增,
单调递增,
综上所述,当![]() 时,
时,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(2)由(1)可得,![]() 最小值为
最小值为![]() ,即
,即![]() ,
,
由题意需证明![]() ,即
,即![]() ,即证明
,即证明![]() ,即证明
,即证明![]() ,
,
令![]() ,对
,对![]() 求导有:
求导有:![]() ,
,
因为![]() ,令
,令![]() 可得:
可得:![]() ,
,
当![]() 时,
时,![]() ,此时
,此时![]() 单调递增,当
单调递增,当![]() 时,
时,![]() ,此时
,此时![]() 单调递减,
单调递减,
所以![]() ,
,
即![]() ,即
,即![]() .
.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目