题目内容
【题目】如图所示,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,求该几何体的表面积(其中∠BAC=30°)及其体积. 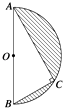
【答案】解:如图所示,过C作CO1⊥AB于O1 , 在半圆中可得∠BCA=90°,∠BAC=30°,AB=2R, ∴AC= ![]() R,BC=R,CO1=
R,BC=R,CO1= ![]() R,
R,
∴S球=4πR2 , ![]() =π×
=π× ![]() R×
R× ![]() R=
R= ![]() πR2 ,
πR2 , ![]() =π×
=π× ![]() R×R=
R×R= ![]() πR2 ,
πR2 ,
∴S几何体表=S球+ ![]() +
+ ![]() =
= ![]() πR2 ,
πR2 ,
∴旋转所得到的几何体的表面积为 ![]() πR2 .
πR2 .
又V球= ![]() πR3 ,
πR3 , ![]() =
= ![]() AO1πCO12=
AO1πCO12= ![]() πR2AO1
πR2AO1![]() =
= ![]() BO1πCO12=
BO1πCO12= ![]() BO1πR2
BO1πR2
∴V几何体=V球﹣( ![]() +
+ ![]() )=
)= ![]() πR3 .
πR3 . 
【解析】求出AC= ![]() R,BC=R,CO1=
R,BC=R,CO1= ![]() R,再求出几何体的表面积;要求旋转后阴影部分的体积即是球的体积减去两个圆锥的体积,根据圆锥的体积公式和球的体积公式进行计算.
R,再求出几何体的表面积;要求旋转后阴影部分的体积即是球的体积减去两个圆锥的体积,根据圆锥的体积公式和球的体积公式进行计算.
【考点精析】通过灵活运用旋转体(圆柱、圆锥、圆台),掌握常见的旋转体有:圆柱、圆锥、圆台、球即可以解答此题.

练习册系列答案
相关题目