题目内容
【题目】正三棱柱ABC﹣A1B1C1的棱长都为2,E,F,G为 AB,AA1 , A1C1的中点,则B1F 与面GEF成角的正弦值( )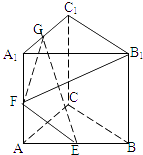
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:取A1B1中点M,连接EM,则EM∥AA1 , EM⊥平面ABC,连接GM
∵G为A1C1的中点,棱长为
∴GM= ![]() B1C1=1,A1G═A1F=1,FG=
B1C1=1,A1G═A1F=1,FG= ![]() ,FE=
,FE= ![]() ,GE=
,GE= ![]()
在平面EFG上作FN⊥GE,则∵△GFE是等腰三角形,∴FN= ![]() ,
,
∴S△GEF= ![]() GE×FN=
GE×FN= ![]() ,
,
S△EFB1=S正方形ABB1A1﹣S△A1B1F﹣S△BB1E﹣S△AFE= ![]() ,
,
作GH⊥A1B1 , GH= ![]() ,
,
∴V三棱锥G﹣FEB1= ![]() S△EFB1×GH=
S△EFB1×GH= ![]() ,
,
设B1到平面EFG距离为h,则V三棱锥B1﹣EFG= ![]() S△GEF=
S△GEF= ![]() ,
,
∵V三棱锥G﹣FEB1=V三棱锥B1﹣EFG ,
∴ ![]() ,
,
∴h= ![]()
设B1F与平面GEF成角为θ,
∵B1F= ![]()
∴sinθ= ![]() =
= ![]()
∴B1F与面GEF所成的角的正弦值为 ![]() .
.
故选A.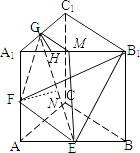
【考点精析】利用空间角的异面直线所成的角对题目进行判断即可得到答案,需要熟知已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则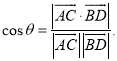 .
.

练习册系列答案
相关题目