Question

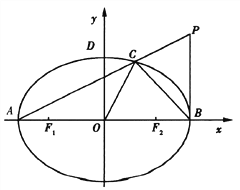
【题目】已知抛物线（），过其焦点作斜率为1的直线交抛物线于， 两点，且，

（1）求抛物线的方程；

（2）已知动点的圆心在抛物线上，且过点，若动圆与轴交于两点，且，求的最小值．

Answer 1

【答案】（1）；（2）.

【解析】试题分析：（1）设直线与抛物线联立方程组，利用韦达定理得到x1+x2=2p，y1+y2=3p，通过|MN|=y1+y2+p=4p=16，求出p，即可求出抛物线C的方程．

（2）设动圆圆心，得，求的表达式，推出x0的范围，然后求解的最小值.

试题解析：

（1）：

联立，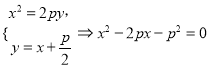

设，则

又因为直线过焦点，则，

所以该抛物线的方程为： ．

（2）设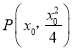，由于圆过点，

则圆P的方程为： ，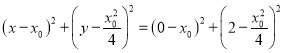

令，则．由对称性， ，不妨，则．

故

由于，

故，（ 时取等）

所以的最小值为．