题目内容
下列命题中,正确命题的个数是( )①命题“?x∈R,使得x3+1<0”的否定是““?x∈R,都有x3+1>0”.
②双曲线
 -
- =1(a>0,a>0)中,F为右焦点,A为左顶点,点B(0,b)且
=1(a>0,a>0)中,F为右焦点,A为左顶点,点B(0,b)且
 =0,则此双曲线的离心率为
=0,则此双曲线的离心率为 .
.③在△ABC中,若角A、B、C的对边为a、b、c,若cos2B+cosB+cos(A-C)=1,则a、c、b成等比数列.
④已知
 ,
, 是夹角为120°的单位向量,则向量λ
是夹角为120°的单位向量,则向量λ +
+ 与
与 -2
-2 垂直的充要条件是λ=
垂直的充要条件是λ= .
.A.1 个
B.2 个
C.3 个
D.4 个
【答案】分析:①利用命题的否定,即可判断其真假;
②利用双曲线的离心率的性质可判断其正误,
③将cosB=-cos(A+C)代入已知,整理可得sinAsinC=sin2B,再利用正弦定理可判断③的正误;
④利用向量的坐标运算与向量垂直的性质可判断其正误.
解答:解:①命题“?x∈R,使得x3+1<0”的否定是““?x∈R,使得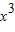 +1≥0”,故①错误;
+1≥0”,故①错误;
②,依题意,F(c,0),A(-a,0),∵点B(0,b),
∴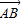 =(a,b),
=(a,b),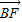 =(c,-b),
=(c,-b),
∵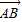 •
•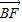 =0,
=0,
∴ac-b2=0,而b2=c2-a2,
∴c2-ac-a2=0,两端同除以a2得:e2-e-1=0,
解得e=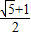 或e=
或e=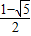 (舍去),
(舍去),
故②正确;
③,在△ABC中,∵A+B+C=180°,
∴cosB=-cos(A+C),
∴原式化为:cos2B-cos(A+C)+cos(A-C)=1,
∴cos(A-C)-cos(A+C)=1-cos2B,
∵cos(A-C)-cos(A+C)=2sinAsinC,1-cos2B=2sin2B,
∴sinAsinC=sin2B,
由正弦定理得:b2=ac,故③a、c、b成等比数列错误;
④,∵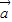 ,
,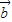 是夹角为120°的单位向量,
是夹角为120°的单位向量,
∴(λ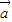 +
+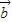 )⊥(
)⊥(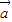 -2
-2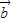 )?(λ
)?(λ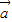 +
+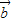 )•(
)•(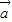 -2
-2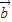 )=0?λ
)=0?λ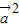 -2
-2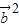 +(1-2λ)
+(1-2λ)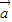 •
•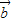 =0?λ-2+(1-2λ)×1×1×(-
=0?λ-2+(1-2λ)×1×1×(- )=0?2λ-2-
)=0?2λ-2- =0,
=0,
∴λ= .故④正确;
.故④正确;
综上所述,正确命题的个数是2个.
故选B.
点评:本题考查命题的真假判断与应用,着重考查命题的否定,向量的坐标运算,考查余弦定理与正弦定理的综合应用,考查双曲线的性质,综合性强,属于难题.
②利用双曲线的离心率的性质可判断其正误,
③将cosB=-cos(A+C)代入已知,整理可得sinAsinC=sin2B,再利用正弦定理可判断③的正误;
④利用向量的坐标运算与向量垂直的性质可判断其正误.
解答:解:①命题“?x∈R,使得x3+1<0”的否定是““?x∈R,使得
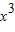 +1≥0”,故①错误;
+1≥0”,故①错误;②,依题意,F(c,0),A(-a,0),∵点B(0,b),
∴
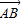 =(a,b),
=(a,b),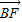 =(c,-b),
=(c,-b),∵
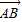 •
•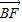 =0,
=0,∴ac-b2=0,而b2=c2-a2,
∴c2-ac-a2=0,两端同除以a2得:e2-e-1=0,
解得e=
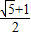 或e=
或e=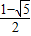 (舍去),
(舍去),故②正确;
③,在△ABC中,∵A+B+C=180°,
∴cosB=-cos(A+C),
∴原式化为:cos2B-cos(A+C)+cos(A-C)=1,
∴cos(A-C)-cos(A+C)=1-cos2B,
∵cos(A-C)-cos(A+C)=2sinAsinC,1-cos2B=2sin2B,
∴sinAsinC=sin2B,
由正弦定理得:b2=ac,故③a、c、b成等比数列错误;
④,∵
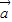 ,
,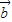 是夹角为120°的单位向量,
是夹角为120°的单位向量,∴(λ
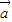 +
+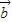 )⊥(
)⊥(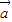 -2
-2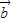 )?(λ
)?(λ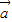 +
+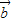 )•(
)•(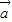 -2
-2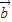 )=0?λ
)=0?λ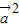 -2
-2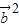 +(1-2λ)
+(1-2λ)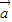 •
•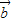 =0?λ-2+(1-2λ)×1×1×(-
=0?λ-2+(1-2λ)×1×1×(- )=0?2λ-2-
)=0?2λ-2- =0,
=0,∴λ=
 .故④正确;
.故④正确;综上所述,正确命题的个数是2个.
故选B.
点评:本题考查命题的真假判断与应用,着重考查命题的否定,向量的坐标运算,考查余弦定理与正弦定理的综合应用,考查双曲线的性质,综合性强,属于难题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目