题目内容
【题目】某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间![]() ,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
,需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
![]()
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(1)求六月份这种酸奶一天的需求量![]() (单位:瓶)的分布列;
(单位:瓶)的分布列;
(2)设六月份一天销售这种酸奶的利润为![]() (单位:元),当六月份这种酸奶一天的进货量
(单位:元),当六月份这种酸奶一天的进货量![]() (单位:瓶)为多少时?
(单位:瓶)为多少时?![]() 的数学期望达到最大值?
的数学期望达到最大值?
【答案】(1)见解析;(2)n=300时,Y的数学期望达到最大值,最大值为520元.
【解析】
(1)由题意知X的可能取值为200,300,500,分别求出相应的概率,由此能求出X的分布列;(2)由题意知这种酸奶一天的需求量至多为500瓶,至少为200瓶,只需考虑200≤n≤500,根据300≤n≤500和200≤n≤300分类讨论经,能得到当n=300时,EY最大值为520元.
(1)由题意知,![]() 所有可能取值为200,300,500,由表格数据知
所有可能取值为200,300,500,由表格数据知
![]() ,
,![]() ,
,![]() .
.
因此![]() 的分布列为
的分布列为
|
|
|
|
| 0.2 | 0.4 | 0.4 |
(2)由题意知,这种酸奶一天的需求量至多为500,至少为200,因此只需考虑 ![]() .
.
当![]() 时,
时,
若最高气温不低于25,则![]() ;
;
若最高气温位于区间![]() ,则
,则![]() ;
;
若最高气温低于20,则![]() ;
;
因此![]() .
.
当![]() 时,
时,
若最高气温不低于20,则![]() ;
;
若最高气温低于20,则![]() ;
;
因此![]() .
.
所以n=300时,Y的数学期望达到最大值,最大值为520元.

【题目】某工厂生产某种型号的农机具零配件,为了预测今年7月份该型号农机具零配件的市场需求量,以合理安排生产,工厂对本年度1月份至6月份该型号农机具零配件的销售量及销售单价进行了调查,销售单价![]() (单位:元)和销售量
(单位:元)和销售量![]() (单位:千件)之间的6组数据如下表所示:
(单位:千件)之间的6组数据如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售单价 | 11.1 | 9.1 | 9.4 | 10.2 | 8.8 | 11.4 |
销售量 | 2.5 | 3.1 | 3 | 2.8 | 3.2 | 2.4 |
(1)根据1至6月份的数据,求![]() 关于
关于![]() 的线性回归方程(系数精确到0.01);
的线性回归方程(系数精确到0.01);
(2)结合(1)中的线性回归方程,假设该型号农机具零配件的生产成本为每件3元,那么工厂如何制定7月份的销售单价,才能使该月利润达到最大?(计算结果精确到0.1)
参考公式:回归直线方程![]() ,
,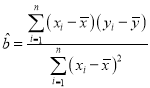
参考数据:![]() ,
,![]()
