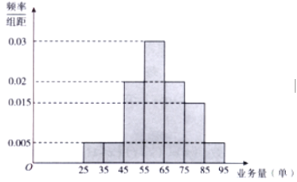
题目内容
【题目】甲、乙两位同学参加数学应用知识竞赛培训,现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,记录如下:
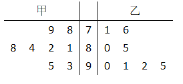
(Ⅰ)分别估计甲、乙两名同学在培训期间所有测试成绩的平均分;
(Ⅱ)从上图中甲、乙两名同学高于85分的成绩中各选一个成绩作为参考,求甲、乙两人成绩都在90分以上的概率;
(Ⅲ)现要从甲、乙中选派一人参加正式比赛,根据所抽取的两组数据分析,你认为选派哪位同学参加较为合适?说明理由.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() (Ⅲ)见解析
(Ⅲ)见解析
【解析】
(Ⅰ)由茎叶图中的数据计算![]() 、
、![]() ,进而可得平均分的估计值;
,进而可得平均分的估计值;
(Ⅱ)求出基本事件数,计算所求的概率值;
(Ⅲ)答案不唯一.从平均数与方差考虑,派甲参赛比较合适;从成绩优秀情况分析,派乙参赛比较合适.
(Ⅰ)由茎叶图中的数据,计算![]() ,
,
![]() ,
,
由样本估计总体得,甲、乙两名同学在培训期间所有测试成绩的平均分分别均约为![]() 分.
分.
(Ⅱ)从甲、乙两名同学高于![]() 分的成绩中各选一个成绩,基本事件是
分的成绩中各选一个成绩,基本事件是![]() ,
,
甲、乙两名同学成绩都在![]() 分以上的基本事件为
分以上的基本事件为![]() ,
,
故所求的概率为![]() .
.
(Ⅲ)答案不唯一.
派甲参赛比较合适,理由如下:
由(Ⅰ)知,![]() ,
,
![]()
![]() ,
,
![]() ,
,
因为![]() ,
,![]() ,
,
所有甲的成绩较稳定,派甲参赛比较合适;
派乙参赛比较合适,理由如下:
从统计的角度看,甲获得![]() 分以上(含
分以上(含![]() 分)的频率为
分)的频率为![]() ,
,
乙获得![]() 分以上(含
分以上(含![]() 分)的频率为
分)的频率为![]() ,
,
因为![]() ,所有派乙参赛比较合适.
,所有派乙参赛比较合适.

【题目】4月23日是“世界读书日”,某中学开展了一系列的读书教育活动.学校为了解高三学生课外阅读情况,采用分层抽样的方法从高三某班甲、乙、丙、丁四个读书小组(每名学生只能参加一个读书小组)学生抽取12名学生参加问卷调查.各组人数统计如下:
小组 | 甲 | 乙 | 丙 | 丁 |
人数 | 12 | 9 | 6 | 9 |
(1)从参加问卷调查的12名学生中随机抽取2人,求这2人来自同一个小组的概率;
(2)从已抽取的甲、丙两个小组的学生中随机抽取2人,用![]() 表示抽得甲组学生的人数,求随机变量
表示抽得甲组学生的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.