题目内容
【题目】为了适应新高考改革，某校组织了一次新高考质量测评（总分100分），在成绩统计分析中，抽取12名学生的成绩以茎叶图形式表示如图，学校规定测试成绩低于87分的为“未达标”，分数不低于87分的为“达标”.
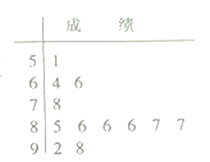
（1）求这组数据的众数和平均数；
（2）在这12名学生中从测试成绩介于80~90之间的学生中任选2人，求至少有1人“达标”的概率.
【答案】（1）86,80.5；（2）
.
【解析】
（1）找出茎叶图中出现次数最多的数为众数，根据平均数公式，即可求得平均数；
（2）在被抽取的学生中，有2个“达标”学生，4个“未达标”学生，按达标和不达标两类编号，列出从6人中任取2人的所有情况，统计出满足条件的基本事件的个数，根据古典概型的概率公式，即可求解.
(1)这组数据的众数为86；
平均数为
.
(2)在被抽取的学生中，有2个“达标”学生，4个“未达标”学生，
将“达标”学生编号为
，
，“未达标”学生编号为
，
，
，
，
则从6人中任取2人,有以下情况：
，
，
，
，
，
，
，
，
，
，
，
，
，
，
.共15种.
其中符合条件的为，，，，，，
，，，共9种.
故至少有1人“达标”的概率
.
练习册系列答案
综合自测系列答案
相关题目
