题目内容
近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机的对入院50人进行了问卷调查得到了如下的列联表:
| | 患心肺疾病 | 不患心肺疾病 | 合计 |
| 男 | | 5 | |
| 女 | 10 | | |
| 合计 | | | 50 |
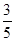 .
.(Ⅰ)请将上面的列联表补充完整;
(Ⅱ)是否有
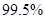 的把握认为患心肺疾病与性别有关?说明你的理由;
的把握认为患心肺疾病与性别有关?说明你的理由;(Ⅲ)已知在患心肺疾病的10位女性中,有3位又患胃病.现在从患心肺疾病的10位女性中,选出3名进行其他方面的排查,记选出患胃病的女性人数为
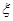 ,求
,求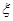 的分布列,数学期望以及方差.
的分布列,数学期望以及方差.下面的临界值表供参考:
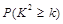 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
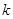 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
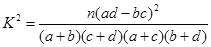 其中
其中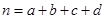 )
)
(Ⅰ)解:列联表补充如下 2分
(Ⅱ)我们有 患心肺疾病 不患心肺疾病 合计 男 20 5 25 女 10 15 25 合计 30 20 50 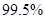 的把握认为是否患心肺疾病是与性别有关系的.
的把握认为是否患心肺疾病是与性别有关系的.
(Ⅲ)分布列如下:
则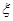
0 1 2 3 
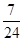

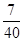
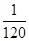
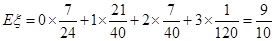

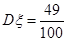
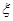 的数学期望及方差分别为
的数学期望及方差分别为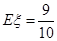 ,
,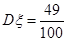
低碳生活,节能减排,控制污染源,控制排放.
解析试题分析:(Ⅰ)解:列联表补充如下 2分 某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据: 某中学共2200名学生中有男生1200名,按男女性别用分层抽样抽出110名学生,询问是否爱好某项运动。已知男生中有40名爱好该项运动,女生中有30名不爱好该项运动。 通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的列联表: (理科)(本小题满分12分)PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,根据现行国家标准GB3095 – 2012,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米 ~ 75毫克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标。从某自然保护区2012年全年每天的PM2.5监测值数据中随机地抽取10天的数据作为样本,监测值频数如下表所示:
(Ⅱ)解:因为 患心肺疾病 不患心肺疾病 合计 男 20 5 25 女 10 15 25 合计 30 20 50 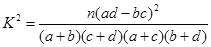 ,所以
,所以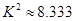
又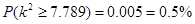 .
.
那么,我们有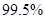 的把握认为是否患心肺疾病是与性别有关系的. 4分
的把握认为是否患心肺疾病是与性别有关系的. 4分
(Ⅲ)解: 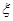 的所有可能取值:0,1,2,3
的所有可能取值:0,1,2,3 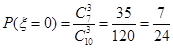 ;
;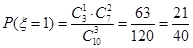 ;
;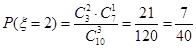 ;
;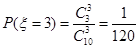 ; 7分
; 7分
分布列如下: 8分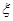
0 1 2 3 
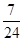


考能大提升系列答案
考前一搏系列答案
考易通初中全程复习导航系列答案

课标新检测系列答案
课程标准同步练习系列答案
课课练习系列答案
云南师大附小一线名师核心试卷系列答案
夺冠计划课时测控系列答案
课时精练系列答案
(I)求销量单价x(元)
8
8.2
8.4
8.6
8.8
9
销量y (件 )
90
84
83
80
75
68
 与单价
与单价 间的回归直线方程;
间的回归直线方程;
(II)预计在今后的销售中,销量与单价仍然服从(I)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?
(1)如下的列联表:
(2)通过计算说明,是否有99%以上的把握认为“爱好该项运动与性别有关”? 参考信息如下:
男
女
总计
爱好
40
不爱好
30
总计
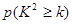
0.050
0.010
0.001
k
3.841
6.635
10.828
性别与看营养说明列联表 单位: 名
(1)根据以上表格,写出 男 女 总计 看营养说明 50 
80 不看营养说明 
20 30 总计 60 50 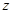
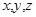 的值.
的值.
(2)根据以上列联表,问有多大把握认为“性别与在购买食物时看营养说明”有关?
(1)从这10天的PM2.5日均值监测数据中,随机抽取3天,求恰有1天空气质量达到一级的概率;(2)从这10天的数据中任取3天数据,记ξ表示抽到PM2.5监测数据超标的天数,求ξ的分布列;(3)以这10天的PM2.5日均值来估计一年的空气质量状况,则一年(按366天算)中平均有多少天的空气质量达到一级或二级。(精确到整数) PM2.5日均值
(微克/立方米)
[25,35]
(35,45]
(45,55]
(55,65]
(65,75]
(75,85]
频数
3
1
1
1
1
3

 是月用水量为[0,2)的家庭代表.
是月用水量为[0,2)的家庭代表. 是月用水量为[2,4]的家庭代表.若从这五位代表中任选两人参加水价听证会,请列举出所有不同的选法,并求家庭代表
是月用水量为[2,4]的家庭代表.若从这五位代表中任选两人参加水价听证会,请列举出所有不同的选法,并求家庭代表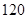 人,其中女性
人,其中女性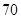 人,男性
人,男性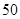 人.女性中有
人.女性中有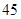 人主要的休闲方式是看电视,另外
人主要的休闲方式是看电视,另外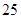 人主要的休闲方式是运动;男性中有
人主要的休闲方式是运动;男性中有 人主要的休闲方式是看电视,另外
人主要的休闲方式是看电视,另外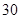 人主要的休闲方式是运动.
人主要的休闲方式是运动.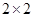 的列联表;
的列联表;
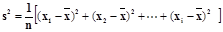 )
)
 的分布列及其数学期望。
的分布列及其数学期望。