题目内容
【题目】已知![]() :
:![]()
![]() ;
; ![]() :直线
:直线![]() 与抛物线
与抛物线![]() 有公共点.如果
有公共点.如果![]() 为真命题,
为真命题,![]() 为假命题,求实数
为假命题,求实数![]() 的取值范围.
的取值范围.
【答案】![]()
【解析】
试题分析:结合二次函数性质可求得p为真命题时的a的取值范围,由直线与抛物线相交的位置关系可求得命题q为真命题时的a的范围,由![]() 为真命题,
为真命题,![]() 为假命题可知两命题一真一假,分两种情况讨论可求得a的取值范围
为假命题可知两命题一真一假,分两种情况讨论可求得a的取值范围
试题解析:![]() 为真
为真![]()
![]()
![]() …………………………………………3分
…………………………………………3分
![]() 为真
为真![]() 直线
直线![]() 与抛物线
与抛物线![]() 有公共点
有公共点
由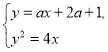 消去
消去![]() ,并整理得
,并整理得
![]() (★)……………………………………4分
(★)……………………………………4分
(1)若![]() ,则
,则![]() 方程(★)变为
方程(★)变为![]() 解得
解得![]() .
.
这时![]() 直线与抛物线有公共点
直线与抛物线有公共点![]() .
.
所以,![]() 使得直线
使得直线![]() 与抛物线
与抛物线![]() 有公共点.……………5分
有公共点.……………5分
(2)若![]() ,则
,则![]()
由直线![]() 与抛物线
与抛物线![]() 有公共点
有公共点
得方程(★)的判别式![]() ,
,
即![]() .解得
.解得![]() .
.
又![]() ,所以
,所以![]() ,或
,或![]() ………………………………………7分
………………………………………7分
综上,若![]() 为真,则
为真,则![]() .…………………………………………………8分
.…………………………………………………8分
如果![]() 为真命题,
为真命题,![]() 为假命题,则
为假命题,则![]() 一真一假.………………………9分
一真一假.………………………9分
当![]() 真
真![]() 假时,则
假时,则![]() 或
或![]() ,且
,且![]() ,所以
,所以![]() ;…………10分
;…………10分
当![]() 假
假![]() 真时,
真时,![]() 或
或![]() ,且
,且![]() ,所以
,所以![]() .…………………11分
.…………………11分
综上,实数![]() 的取值范围为
的取值范围为![]() ………………………………………12分[来
………………………………………12分[来

练习册系列答案
相关题目