题目内容
(本小题满分12分)
设命题 :函数
:函数 在
在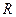 上单调递减
上单调递减
命题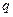 :关于
:关于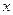 不等式
不等式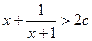 对于
对于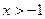 恒成立
恒成立
如果 是真命题,
是真命题,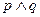 是假命题,求
是假命题,求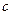 的范围.
的范围.
设命题
 :函数
:函数 在
在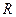 上单调递减
上单调递减命题
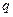 :关于
:关于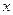 不等式
不等式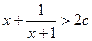 对于
对于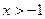 恒成立
恒成立如果
 是真命题,
是真命题,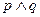 是假命题,求
是假命题,求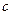 的范围.
的范围.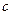 的范围是
的范围是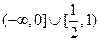
 :函数
:函数 在
在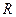 上单调递减,即
上单调递减,即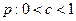
因为
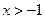 ,所以
,所以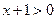 ,
,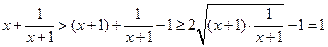
当
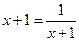 ,即
,即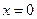 时
时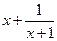 有最小值1,所以
有最小值1,所以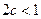 ,
,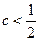
故
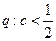
因为
 是真命题,
是真命题,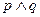 是假命题,所以
是假命题,所以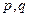 中一个真命题,一个假命题
中一个真命题,一个假命题当
 是真命题,
是真命题,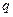 是假命题时
是假命题时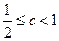 ,
,当
 是假命题,
是假命题,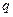 是真命题时
是真命题时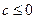
所以,
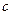 的范围是
的范围是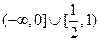

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
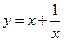 在
在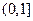 上是减函数,在
上是减函数,在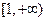 上是增函数;
上是增函数; 在
在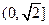 上是减函数,在
上是减函数,在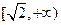 上是增函数;
上是增函数; 
 在
在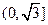 上是减函数,在
上是减函数,在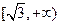 上是增函数;
上是增函数; 的值域是
的值域是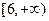 ,则实数
,则实数 的值是___________.
的值是___________.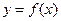 在定义域
在定义域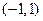 上是减函数,且
上是减函数,且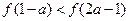 ,则
,则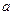 的取值范围是 。
的取值范围是 。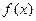 是R上的增函数,
是R上的增函数,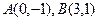 是其图象上的两点,记不等
是其图象上的两点,记不等 的解集
的解集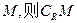 =( )
=( )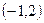
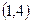
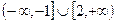
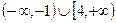
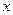 规定
规定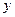 取
取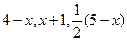 三个值中的最小值,则函数
三个值中的最小值,则函数 在
在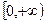 上为增函数”的充分必要条件是( )
上为增函数”的充分必要条件是( )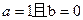
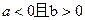
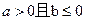

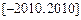 上的函数
上的函数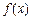 满足:对于任意
满足:对于任意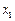 ,
,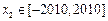 ,有
,有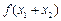
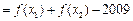 .设
.设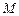 ,
,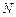 ,则
,则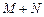 的值为( )
的值为( )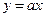 和
和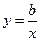 在(0,+
在(0,+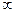 )上都是减少的,则
)上都是减少的,则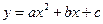 在(-
在(-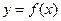 是定义在
是定义在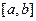 上的增函数,其中
上的增函数,其中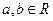 且
且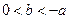 ,已知
,已知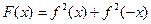 ,则对于
,则对于
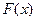 有以下四个说法:
有以下四个说法: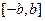 ;②是偶函数;③最小值是0;④在定义域内单调递增.
;②是偶函数;③最小值是0;④在定义域内单调递增.