题目内容
【题目】在圆![]() 上任取一点
上任取一点![]() ,过点
,过点![]() 向
向![]() 轴作垂线段
轴作垂线段![]() ,垂足为
,垂足为![]() ,当点
,当点![]() 在圆上运动时,线段
在圆上运动时,线段![]() 的中点
的中点![]() 的轨迹为
的轨迹为![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() (0,-2)作直线
(0,-2)作直线![]() 与
与![]() 交于
交于![]() 两点,(O为原点),求三角形
两点,(O为原点),求三角形![]() 面积的最大值,并求此时的直线
面积的最大值,并求此时的直线![]() 的方程.
的方程.
【答案】(1)![]() (2)最大面积为1,
(2)最大面积为1,![]() 方程为
方程为![]()
【解析】
(1)利用代入法求曲线![]() 的方程.(2)先求出三角形
的方程.(2)先求出三角形![]() 面积的解析式和k的范围,再求其最大值和此时直线的方程.
面积的解析式和k的范围,再求其最大值和此时直线的方程.
(1)设M(x,y)是曲线C上任一点,
因为PQ⊥x轴,M是PQ的中点,所以点P的坐标为(x,2y).
因为点P在圆x2+y2=4上,所以x2+(2y)2=4.
所以曲线C的方程是![]() +y2=1.
+y2=1.
(2当直线l的斜率不存在时显然不符合题意;
当直线l的斜率存在时,设直线l的方程为y=kx-2,与椭圆交于A(x1,y1),B(x2,y2)两点,
由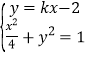 得(1+4k2)x2-16kx+12=0,
得(1+4k2)x2-16kx+12=0,
由Δ=162k2-48(1+4k2)>0,得k2>![]() .
.
所以x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
因为S△OAB=![]() |OD||x1-x2|=|x1-x2|=
|OD||x1-x2|=|x1-x2|=![]()
=4![]() .令4k2-3=t,则4k2=t+3(由上可知t>0),
.令4k2-3=t,则4k2=t+3(由上可知t>0),
SOANB=4![]() =4
=4![]() ,
,
当且仅当t=4,即k2=![]() 时取等号;
时取等号;
所以当k=±![]() 时三角形OAB面积的最大值为1,
时三角形OAB面积的最大值为1,
此时直线l的方程为y=±![]() x-2.
x-2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

